Детерминированный анализ

Интегральный метод в экономике

Интегральный метод как бы обобщает метод цепных подстановок. Однако, его преимуществом является тот факт, что он не оказывает влияние на конечный результат исследования. Этот метод требует знаний в области математики, а также проведения большого числа вычислений, по сравнению с другими методами.

Элиминирование, которое часто применяется в факторном анализе, не учитывает взаимного влияния факторов друг на друга. Поэтому при его влиянии результат получает большее отклонение от реальной величины. Именно для того, чтобы избежать этого отклонения используется интегральный метод факторного анализа. В этом случае расположение факторов в модели не влияет на конечный результат исследовании. Кроме того, общий прирост результата под влиянием факторов распределяется в равных долях между всеми воздействующими переменными.

Чтобы повысить результативность анализа прирост рассматривается на отдельных временных промежутках, так как факторы могут иметь разную направленность воздействия. Таким образом, появляется возможность проанализировать приращение результата на малых временных отрезках. Итогом вычислений станет число, получаемого в результате суммирования результатов приращения.

Как правило, интегральный метод осуществляется с помощью вычислительной техники. От исследователя требует завести прединтегральные данные. Для практической деятельности часто применяют специальные рабочие формулы, которые позволяют учитывать факторную разнонаправленность. Эти данные приведены в специальной литературе, что очень облегчает процесс анализа. То есть, специалист подставляет в рабочие формулы фактические данные, а затем осуществляет расчеты. Таким образом, достигается наибольшая точность вычислений.

Интегральный метод не требует приемов, помогающих распределить неразложимый остаток, так как благодаря логарифмическому закону в нем автоматически осуществляется перераспределение факторов. С другой стороны, этот метод позволяет разложить показатель результата по факторам, что делает его универсальным в различных видах математических моделей.

Так и не нашли ответ на свой вопрос?

Просто напиши с чем тебе нужна помощь

Пример применения интегрального способа для факторного анализа

Порядок применения интегрального способа рассмотрим на следующем примере. Проанализировать влияние на валовый объем производства количества работников и их выработки интегральным способом. Исходные данные представлены в таблице.

Показатель	Условное обозначение	Базисное значение (0)	Фактическое значение (1)	Изменение (+,-)
Абсолютное	Относительное, %
Объем валовой продукции, тыс. руб.	ВП	2920	3400	+480	16,40
Среднесписочная численность персонала, чел.	ЧР	20	25	+5	25,00
Среднегодовая выработка продукции одним работником, тыс. руб.	ГВ	146	136	-10	-6,85

Решение. Зависимость объема производства продукции от данных факторов можно описать с помощью двухфакторной мультипликативной модели: ВП = ЧР * ГВ.

Алгоритм расчета влияния факторов интегральным способом таков:

• ΔВП(ЧР) = ΔЧР*ГВ0+½ΔЧР*ΔГВ = 5*146+0,5*5*(-10) = 705 тыс. руб. – влияние изменения численности персонала на объем производства;
• ΔВП(ГВ) = ΔГВ*ЧР0+½ΔЧР*Δ(-10) = -10*20+0,5*5*(-10) = -225 тыс. руб. – влияние изменения среднегодовой выработки продукции одним работником на объем производства;
• ΔВП = ΔВП(ЧР)+ ΔВП(ГВ) = 705 + (-225) = 480 тыс. руб. – суммарное влияние двух факторов.

Таким образом, использование интегрального метода знания основ интегрирования. Достаточно в готовые рабочие формулы подставить числовые данные и сделать расчеты.

ФАКТОРНЫЙ АНАЛИЗ: ОБЩАЯ ХАРАКТЕРИСТИКА И СПОСОБЫ ПРОВЕДЕНИЯ

Факторный анализ — это способ комплексного и системного исследования влияния отдельных факторов на размер итоговых показателей. Основная цель проведения такого анализа — найти способы увеличить доходность фирмы.

Факторный анализ позволяет определить общее изменение прибыли в текущем периоде по отношению к предыдущему (базовому) периоду или изменение фактических показателей прибыли по отношению к плану, а также влияние на эти изменения следующих факторов:

• объем продажи продукции;
• себестоимость реализуемой продукции;
• цены реализации;
• ассортимент реализуемой продукции.

Таким образом, с помощью факторного анализа можно установить объем продаж, себестоимость или цену реализации, которые увеличат прибыль компании, а факторный анализ по ассортименту реализуемой продукции даст возможность выявить товар, который продается лучше всего, и товар, пользующийся наименьшим спросом.

Показатели для факторного анализа берут из бухгалтерского учета. Если анализируют итоги за год, то используют данные формы № 2 «Отчет о финансовых результатах».

Факторный анализ можно проводить:

1) способом абсолютных разниц;

2) способом цепных подстановок.

Математическая формула модели факторного анализа прибыли от продаж:

ПР = V_прод × (Ц – S_ед),

где ПР — прибыль от продаж (плановая или базовая);

V_прод — объем продаж продукции (товаров) в натуральных величинах (штуки, тонны, метры и т. д.);

Ц — продажная цена единицы реализованной продукции;

S_ед — себестоимость единицы реализованной продукции.

Способ абсолютных разниц

За основу факторного анализа берется математическая формула ПР (прибыль от продаж). Формула включает три анализируемых фактора:

• объем продаж в натуральных единицах;
• цену;
• себестоимость одной единицы продаж.

Рассмотрим ситуации, влияющие на прибыль. Определим изменение величины прибыли за счет каждого фактора. Расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей. Приведем формулы расчета для каждой ситуации, оказавшей влияние на прибыль.

Ситуация 1. Влияние на прибыль объема продаж:

ΔПР_объем = ΔV_прод × (Ц_план – S_{ед. план}) = (V_{прод. факт} – V_{прод. план}) × (Ц_план – S_{ед. план}).

Ситуация 2. Влияние на прибыль продажной цены:

ΔПР_цена = V_{прод. факт} × ΔЦ = V_{прод. факт} × (Ц_факт – Ц_план).

Ситуация 3. Влияние на прибыль себестоимости единицы продукции:

ΔПР_Sед = V_{прод. факт} × (–ΔS_ед) = V_{прод. факт} × (–(S_{ед. факт} – S_{ед. план})).

Способ цепной подстановки

Используя такой метод, сначала рассматривают влияние одного фактора при неизменности прочих, затем второго и т. д. За основу берут все ту же математическую формулу модели факторного анализа прибыли от продаж.

Выявим влияние факторов на сумму прибыли.

Ситуация 1. Изменение объема продаж.

ПР1 = V_{прод. факт} × (Ц_план – S_{ед. план});

ΔПР_объем = ПР1 – ПР_план.

Ситуация 2. Изменение цены продаж.

ПР2 = V_{прод. факт} × (Ц_факт – S_{ед. план});

ΔПР_цена = ПР2 – ПР1.

Ситуация 3. Изменение себестоимости продаж единицы продукции.

ПР_Sед = V_{прод. факт} × (Ц_факт – S_{ед. факт});

ΔПР_Sед = ПР3 – ПР2.

Условные обозначения, применяемые в приведенных формулах:

ПР_план — прибыль от реализации (плановая или базовая);

ПР1 — прибыль, полученная под влиянием фактора изменения объема продаж (ситуация 1);

ПР2 — прибыль, полученная под влиянием фактора изменения цены (ситуация 2);

ПР3 — прибыль, полученная под влиянием фактора изменения себестоимости продаж единицы продукции (ситуация 3);

ΔПР_объем — сумма отклонения прибыли при изменении объема продаж;

ΔПР_цена — сумма отклонения прибыли при изменении цены;

ΔП_Sед — сумма отклонения прибыли при изменении себестоимости единицы реализованной продукции;

ΔV_прод — разница между фактическим и плановым (базисным) объемом продаж;

ΔЦ — разница между фактической и плановой (базисной) ценой продаж;

ΔS_ед — разница между фактической и плановой (базисной) себестоимостью единицы реализованной продукции;

V_{прод. факт} — объем продаж фактический;

V_{прод. план} — объем продаж плановый;

Ц_план — цена плановая;

Ц_факт — цена фактическая;

S_{ед. план} — себестоимость единицы реализованной продукции плановая;

S_{ед. факт} — себестоимость единицы реализованной продукции фактическая.

Замечания

1. Способ цепной подстановки дает те же результаты, что и способ абсолютных разниц.
2. Суммарное отклонение прибыли будет равно сумме отклонений под влиянием всех факторов, по которым проводят факторный анализ.

4.1. Метод цепных подстановок

Метод цепных подстановок заключается в определении ряда промежуточных значений результативного показателя путем последовательной замены базисных значений факторов на отчетные. Данный способ основан на элиминировании. Элиминировать — значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Предполагается, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения, потом изменяются два при неизменности остальных и т.д.

В общем виде применение способа цепных постановок можно описать следующим образом:

где a, b, c — базисные значения факторов, оказывающих влияние на обобщающий показатель у;a₁ , b₁, c₁ — фактические значения факторов;y_a, y_b, — промежуточные изменения результирующего показателя, связанного с изменением факторов а, b соответственно.

Общее изменение Δу = у₁ — у складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

Рассмотрим пример. Исходные данные для факторного анализа сведены в таблицу 4.1. На основе этих данных проведем описанным выше способом анализ влияния на объем товарной продукции количества работников и их выработки.

Таблица 4.1

Исходные данные для факторного анализа

Показатели	Услов. обозн-я	Базисные значения (0)	Фактические значения (1)	Изменение
Абсолютное (+,- )	Относительное (%)
Объем товарной продукции, тыс. руб.	ТП	2920	3400	+480	116,40
Количество работников, чел	Ч	20	25	+5	125,00
Выработка на одного работающего, тыс. руб.	СВ	146	136	-10	93,15

Зависимость объема товарной продукции от данных факторов можно описать с помощью мультипликативной модели:

ТП  = Ч — СВ,

ТП  =  Ч · CB = 20 — 146 = 2920 (тыс. руб.).

Тогда   влияние   изменения   величины   количества   работников на обобщающий показатель можно рассчитать по формуле:

ТПусл₁ = Ч₁ — СВ = 25 — 146 = 3650 (тыс. руб.),

ΔТПусл₁ = ТПусл₁ — ТП0 = 3650 — 2920 = 730 (тыс. руб.).

Далее   определим   влияние   изменения   выработки   работников на обобщающий показатель:

ТП₁ = Ч₁ · СВ₁  =  25 · 136  =  3400 (тыс. руб.)

ΔТПусл₂ = ТП₁ — ТПусл₁ = 3400 — 3650 = — 250 (тыс. руб.)

Таким образом, на увеличение объема товарной продукции на 730 тыс. руб. положительное влияние оказало изменение на 5 человек численности работников. Отрицательное влияние оказало снижение выработки на 10 тыс. руб., что вызвало снижение объема на 250 тыс. руб. Суммарное влияние двух факторов привело к увеличению объема продукции на 480 тыс. руб.

Преимущества данного способа: универсальность применения, простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки:

• при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов;
• если модель представлена несколькими количественными и качественными показателями, то в первую очередь определяется влияние факторов первого порядка, затем второго и т.д.

Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.).

Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, средняя продолжительность рабочего дня и т.д.).

Пример применения способа относительных разниц

Порядок применения способа относительных (процентных) разниц рассмотрим на следующем примере. Проанализировать влияние на валовый
объем производства количества работников, количества отработанных дней одним работником и их выработки способом относительных разниц. Исходные данные
представлены в таблице.

Показатель	Условное обозначение	Базисное значение (0)	Фактическое значение (1)	Абсолютное изменение (+,-)
Объем валовой продукции, тыс. руб.	ВП	2920	3380	+460
Среднесписочная численность персонала, чел.	ЧР	20	25	+5
Количество отработанных дней одним работником за год	Д	200	208	+8
Среднедневная выработка продукции одним работником, тыс. руб.	ДВ	0,73	0,65	-0,08

Решение. Зависимость объема производства продукции от данных
факторов выражается трехфакторной мультипликативной моделью:ВП = ЧР * Д*ДВ.

Алгоритм расчета способом относительных разниц таков:

• Определяем относительные отклонения рассматриваемых факторов:
  ΔЧР% = ((ЧР1-ЧР0)/ЧР0)*100% = ((25-20)/20)*100% = 25%;
  ΔД% = ((Д1-Д0)/Д0)*100% = ((208-200)/200)*100% = 4%;
  ΔДВ% = ((ДВ1-ДВ0)/ДВ0)*100% = ((0,65-0,73)/0,73)*100% = -10,96%;
• Рассчитаем влияние каждого фактора на валовый объем производства:
  ΔВП(ЧР) = ВП0* ΔЧР%/100 = 2920*25/100 = 730 тыс. руб. — влияние изменения количества работников;
  ΔВП(Д) = (ВП0+ΔВП(ЧР))* ΔД%/100 = (2920+730)*4/100 = 146 тыс. руб. — влияние изменения количества отработанных
  дней одним работником;
  ΔВП(ДВ) = (ВП0+ΔВП(ЧР)+ΔВП(Д))*ΔДВ%/100 = (2920+730+146)*(-10,96)/100 = -416,04 ≈ -416 тыс. руб. — влияние
  изменения величины среднедневной выработки продукции одним работником;
• Суммарное влияние трех факторов определим по формуле:
  ΔВП = ΔВП(ЧР) + ΔВП(Д) + ΔВП(ДВ) = 730+146+(-416) = 460 тыс. руб. — значение совпадает с табличным и подтверждает
  правильность расчетов.

Вывод. Таким образом, на изменение объема производства продукции положительное влияние оказало
увеличение на 5 человек численности работников, что вызвало увеличение объема производства на 730 тыс. руб. и увеличение количества
отработанных дней на 8 каждым работником, что вызвало увеличение объема производства на 146 тыс. руб.
Отрицательное влияние оказало снижение среднедневной выработки на 80 руб., что вызвало снижение объема производства на 416 тыс. руб.
Суммарное влияние трех факторов привело к увеличению объема производства на 460 тыс. руб.

Детерминированный анализ

Классификация математических приемов, используемых в анализе финансово-хозяйственной деятельности.

Детерминированный анализ — это разложение исследуемого явления ( показателей эффективности работы) на прямые факторы, т.е. факторы, влияние которых можно количественно соизмерить, построив модель непрерывной цепи связей.
 

Детерминированный анализ предполагает разработку моделей, в которых количество факторов определяется длиной непрерывной цепи прямых связей, путем логического отбора и качественного анализа.
 

Детерминированный анализ применяется для исследования функциональных взаимосвязей между факторными и результативными показателями.
 

В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
 

В детерминированном анализе для измерения влияния факторов на результативный показатель используют разные способы, в том числе цепной подстановки, абсолютных и относительных разниц, индексный, пропорционального деления, долевого участия, интегральный и др. В основе нескольких первых из названных способов лежит прием элиминирования, позволяющий устранить влияние всех других факторов, кроме одного, влияние которого измеряется в данный момент.
 

В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
 

В детерминированном анализе для измерения влияния факторов на результативный показатель используют разные способы, в том числе цепной подстановки, абсолютных и относительных разниц, индексный, пропорционального деления, долевого участия, интегральный и др. В основе нескольких первых из названных способов лежит прием элиминирования, позволяющий устранить влияние всех других факторов, кроме одного, влияние которого измеряется в данный момент.
 

В-третьих, детерминированный анализ может выполняться для единичного объекта в отсутствие совокупности наблюдений.
 

Статистический и детерминированный анализ существующих и вновь проектируемых САУ не может быть проведен без наличия математической модели газосборного коллектора, являющегося наиболее сложным и наименее изученным звеном газового промысла.
 

Обзор методов детерминированного анализа начинаем с ючных методов, применимых лишь к частным видам дифференциальных уравнении.
 

В системе R1 детерминированный анализ используется только в отношении части з &-дач, которые всегда выполняются в одном и том же порядке. Достигается такое упрощение следующим образом.
 

Если результаты прямого детерминированного анализа должны получиться точными и однозначными, то стохастического — с некоторой вероятностью ( надежностью), которую следует оценить.
 

Рассмотрим сначала задачу детерминированного анализа в следующей постановке.
 

Если результаты прямого детерминированного анализа должны получиться точными и однозначными, то стохастического — с некоторой вероятностью ( надежностью), которую следует оценить.
 

Особенности факторного анализа методом логарифмирования

Данный метод успешно применяется в отношении мультипликативных моделей. Он является одним из точнейших вариантов оценки воздействия факторов.

Особенностью логарифмического метода факторного анализа является то, что здесь учитывают не абсолютные приросты (динамику) показателей, а индексы роста (снижения). Помимо этого, прирост от взаимодействия факторов на конечный результат распределяется пропорционально доле каждого из них, что позволяет установить точные значения воздействия. Единственным недостатком логарифмического способа является его «узость», так как он применяется далеко не всегда, а исключительно в отношении мультипликативных моделей.

В математическом ракурсе метод логарифмирования выглядит следующим образом.

Рассмотрим функцию

Прологарифмируем ее, тогда она будет выглядеть как:

Индекс изменения показатель отражает ту же зависимость, что проявляется между ними. Поэтому можно произвести замену:

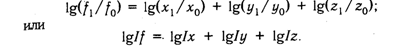
Далее необходимо разделить обе части на , а затем умножить на . После этого функция обреете новый вид:

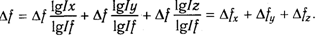
Исходя из этого, можно сделать вывод, что влияние факторов определяется по формулам:

Пример применения логарифмического способа

Таким образом, рассмотренные методы позволяют получить более точные результаты анализа и корректно составить план дальнейших действий на ближайшую перспективу. Для их успешного использования специалист должен не только разбираться в факторных моделях, но и хорошо владеть математическими операциями интегрирования и логарифмирования, понимать суть соответствующих методов и возможности использования.

Детерминированный факторный анализ

Для проведения детерминированного факторного анализа используют несколько моделей:

• кратную;
• адаптивную;
• мультипликативную.

В процессе осуществления вычислений при помощи каждой из них используют данные об исследуемых факторах, а также конечный результат.

Модель детерминированного факторного анализа	Формула	Расшифровка формулы
Кратная	А / А1	А, А1 – факторы
Адаптивная	А + А1 + А2 + … +Ан	А, А1, А2, Ан – факторы
Мультипликативная	А * А1 * А2 * … *Ан	А, А1, А2, Ан – факторы

То есть, детерминированный факторный анализ проводится путем нахождения частного от исследуемых факторов, их произведения или суммы.

Методы детерминированного факторного анализа

Детерминированный факторный анализ проводят при помощи следующих методов:

• цепных постановок;
• логарифмирования;
• абсолютных разниц;
• интегрального;
• относительных разниц.

Для получения достоверного результата, нужно тщательно отобрать факторы, которые непосредственно влияют на конечный результат деятельности.

Метод цепных постановок

Метод цепных подстановок представляет собой последовательную замену одного из показателей прошлого периода с отчетным. При этом все остальные факторы остаются нетронутыми. Изменяя показатель, необходимо проводить новый расчет.

Для анализа используют факторную модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Чтобы определить взаимосвязь между факторами и конечным результатом, необходимо найти разницу между результатами расчетов. Для этого из итога второго расчета нужно отнять результат первого, из третьего – второго, из четвертого – третьего и так далее

В процессе исследования важно соблюдать строгую последовательность, в противном случае, анализ может показать некорректную информацию

Метод логарифмирования

Метод логарифмирования считается одним из наиболее точных способов факторного анализа. Он заключается в составлении логарифма на основании показателей прошлого и отчетного периода.

Для этого находят сумму всех факторов, затем записывают алгебраическое выражение в виде произведения отношения фактических факторов к плановым. А уже на основании него составляют логарифм.

Метод абсолютных разниц

Основой для вычисления методом абсолютных разниц служит факторная модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Но для начала нужно найти абсолютные отклонения. Для этого из факторов базисного периода отнимают плановые показатели.

Для определения взаимосвязи между ними необходимо провести анализ при помощи факторной модели, заменяя относительные результаты на абсолютные отклонения.

Интегральный метод

Интегральный метод используется только тогда, когда конечный результат можно представить в виде функции от нескольких показателей. Интегральное выражение показывает зависимость функции от аргументов.

Метод относительных разниц

Метод относительных разниц используется для измерения влияния факторов на динамику конечного результата в мультипликативных и смешанных моделях. Он применяется в том случае, если данные для расчета выражены в относительных отклонения факторных показателей (процентах).

При проведении анализа данным методом за основу берется факторная модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Относительные отклонения находят по формуле:

(Аф – Ап) / Ап,

где Аф – фактический показатель;

Ап – плановый или базисный показатель.

Факторный анализ рентабельности

ФА рентабельности проводится для анализа рациональности распределения ресурсов. В результате можно определить, какие факторы наибольшим образом влияют на конечный результат. В результате можно оставить только те факторы, которые наилучшим образом воздействуют на эффективность. На основании полученных данных можно изменить ценовую политику компании. На себестоимость продукции могут влиять следующие факторы:

• постоянные издержки;
• переменные издержки;
• прибыль.

Уменьшение издержек провоцирует повышение прибыли. При этом себестоимость не изменяется. Можно сделать вывод о том, что на прибыльность влияют имеющиеся издержки, а также объем проданной продукции. Факторный анализ позволяет определить степень влияния этих параметров. Когда имеет смысл его проводить? Основной повод к проведению – уменьшение или повышение прибыльности.

Факторный анализ проводится посредством следующей формулы:

Rв= ((Вт-СБ -КРБ-УРБ)/ Вт) — (ВБ-СБ-КРБ-УРБ)/ВБ, где:

ВТ – выручка за нынешний период;

СБ – себестоимость за нынешний период;

КРБ – коммерческие траты за нынешний период;

УРБ – управленческие траты за предшествующий период;

ВБ – выручка за предшествующий период;

КРБ – коммерческие траты за предшествующий период.

Иные формулы

Рассмотрим формулу расчета степени воздействия себестоимости на прибыльность:

Rс= ((Вт-СБот -КРБ-УРБ)/ Вт) — (Вт-СБ-КРБ-УРБ)/Вт,

СБот – это себестоимость продукции за нынешний период.

Формула для расчета влияния управленческих трат:

Rур= ((Вт-СБ -КРБ-УРот)/ Вт) — (Вт-СБ-КРБ-УРБ)/Вт,

УРот – это управленческие траты.

Формула для вычисления степени воздействия коммерческих издержек:

Rк= ((Вт-СБ -КРо-УРБ)/ Вт) — (Вт-СБ-КРБ-УРБ)/Вт,

КРо – это коммерческие траты за предыдущее время.

Совокупное воздействие всех факторов высчитывается по следующей формуле:

Rоб=Rв+Rс+Rур+Rк.

ВАЖНО! При расчетах имеет смысл высчитывать влияние каждого фактора в отдельности. Результаты общего ФА имеют небольшую ценность

Пример

Рассмотрим показатели организации за два месяца (за два периода, в рублях). В июле доход организации составил 10 тысяч, себестоимость продукции – 5 тысяч, административные траты – 2 тысячи, коммерческие траты – 1 тысяча. В августе доход компании составил 12 тысяч, себестоимость продукции – 5,5 тысяч, административные траты – 1,5 тысячи, коммерческие траты – 1 тысяча. Проводятся следующие расчеты:

R=((12 тысяч-5,5 тысяч-1 тысяча-2 тысячи)/12 тысяч)-((10 тысяч- 5,5 тысяч-1 тысяча-2 тысячи)/10 тысяч)=0,29-0,15=0,14

Из этих расчетов можно сделать вывод о том, что прибыль организации повысилась на 14%.

Понятие факторного анализа

Факторный анализ – это метод изучения взаимосвязей между переменными значениями.

Считается, что переменные, которые известны исследователю, находятся в зависимости от меньшего числа факторов и имеют меньшую тенденцию к проявлению ошибок. С помощью этого метода математического исследования можно решить две глобальных задачи:

1. Сформировать всестороннее описание объекта, а затем скомпоновать его.
2. Выявить скрытые факторы, которые влияют на линейную взаимосвязь изучаемых объектов и явлений.

Применение факторного анализа позволяет реализовать сразу несколько целей исследования. Прежде всего, он помогает установить взаимосвязи между переменными, а также сократить их число для описания зависимости. Для удобства схожие факторы группируют, что облегчает модель, а также делает ее более наглядной. При объединении факторов их влияние на объект будет выше, а значит, ярче проявятся свойства, связанные с его изменениями.

Группировка позволяет отследить скрытые факторы влияния

Это свойство особенно важно при исследовании социально-экономических явлений. Именно скрытые переменные, проявляющиеся в изменении объектов, называются факторами

Попробуй обратиться за помощью к преподавателям

Чтобы определить наиболее значимые факторы применяются метод главных компонент. Его сущность заключается в замене взаимосвязанных величин не связанными между собой факторами. Для упрощения интерпретации результатов из уравнения могут исключаться менее информативные данные. Метод главных компонент является единственным математически обоснованным методом факторного анализа.

Факторный анализ имеет несколько форм. Он может быть разведочным, то есть направленным на выявление скрытых факторов. Конфирматорный анализ подтверждает гипотезы, относящиеся к исследованию числа факторов и оказываемых ими нагрузках.

Понятие факторного анализа

Факторный анализ – это многомерная методика, позволяющая изучить взаимосвязи между параметрами переменных. В процессе происходит исследование строения ковариационных или корреляционных матриц. Факторный анализ используется в самых различных науках: психометрике, психологии, экономике. Основы этого метода были разработаны психологом Ф. Гальтоном.

Как учетная политика влияет на прибыль?

Задачи проведения

Для получения достоверных результатов лицу требуется сравнить показатели по нескольким шкалам. В процессе определяется корреляция полученных значений, их сходство и различия. Рассмотрим базовые задачи факторного анализа:

• Обнаружение существующих значений.
• Подбор параметров для полноценного анализа значений.
• Классификация показателей для системной работы.
• Обнаружение взаимосвязей между результативными и факторными значениями.
• Определение степени влияния каждого из факторов.
• Анализ роли каждого из значений.
• Применение факторной модели.

Исследован должен быть каждый параметр, который влияет на итоговое значение.

Интегральный способ детерминированного факторного анализа

Как известно, в детерминированном факторном анализе используют следующие основные способы:

• способ цепных подстановок;
• способ абсолютных разниц;
• способ относительных (процентных) разниц;
• интегральный метод и др.

Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер – применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях.

Использование этого способа позволяет получить более точные результаты по сравнению с остальными выше названными способами, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.

Рассмотрим алгоритмы расчетов влияния факторов для различных моделей, приводимые в специальной литературе:

Мультипликативная модель вида f = x*y:

Δf(x) = Δx*y0 + ½Δx*Δy, или Δf(x) = ½Δx (y0 + y1); Δf(y) = Δy*x0 + ½Δx*Δy, или Δf(y) = ½Δy (x0 + x1); где x0, y0 – базисные (плановые) значения факторов, оказывающих влияние на результативный показатель; x1, y1 — фактические значения факторов; Δx = x1-x0, Δy = y1-y0 — абсолютные изменения (отклонения) факторов х, у соответственно;

Мультипликативная модель вида f = x*y*z:

Δf(x) = ½Δx (y0*z1 + y1*z0) + ⅓Δx*Δy*Δz; Δf(y) = ½Δy (x0*z1 + x1*z0) + ⅓Δx*Δy*Δz; Δf(z) = ½Δz (x0*y1 + x1*y0) + ⅓Δx*Δy*Δz;

Кратная модель вида f = x/y:

Δf(x) = Δx/Δy * ln |y1/y0|; Δf(y) = Δf — Δf(x) = (f1-f0) — Δf(x);

Смешанная модель вида f = x/(y+z):

Δf(x) = Δx/(Δy+Δz) * ln |(y1+z1)/(y0+z0)|; Δf(y) = (Δf — Δf(x))Δy / (Δy+Δz); Δf(z) = (Δf — Δf(x))Δz / (Δy+Δz).