Факторный анализ, его виды и методы

Факторный анализ

Определение

Факторный анализ  – это процедура, с помощью которой большое число переменных, сводится к меньшему количеству независимых влияющих величин, называемых факторами. При этом в один фактор объединяются переменные (признаки), сильно коррелирующие (связанные) между собой. Переменные (признаки), относящиеся к разным факторам слабо коррелируют между собой.

Области применения факторного анализа

Факторный анализ используется при исследовании сложных объектов и систем (например, в психологии, биологии, социологии, экономике и др.) в том случае, когда напрямую невозможно измерять величины, определяющие свойства этих объектов (так называемые факторы). Однако для измерения доступны другие величины (переменные, признаки), которые зависят от этих факторов. Иными словами, фактор, который мы не можем измерить напрямую, проявляется в изменении нескольких переменных.

В области физической культуры и спорта в роли переменных могут выступать результаты тестирования уровня технической, физической, тактической подготовленности спортсменов, а также результаты медико-биологических и педагогических исследований.

Виды факторного анализа

Существует два основных вида факторного анализа – эксплораторный (исследовательский, разведочный) и конфирматорный (подтверждающий гипотезу).

Более подробно о методах статистической обработки данных рассказано в книгах:

• «Факторный анализ в педагогических исследованиях в области физической культуры и спорта»
• «Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта»
• «Компьютерная обработка данных экспериментальных исследований»

Эксплоаторный факторный анализ

Эксплораторный факторный анализ проводится на ранних этапах исследования, когда почти ничего не известно о структуре изучаемого явления и имеется значительное количество исходных данных. Цель проведения такого анализа – выявление латентной внутренней структуры и снижение размерности, то есть сокращение количества исследуемых переменных за счет объяснения их через новые факторные переменные. В ходе этого анализа, если необходимо, формулируются гипотезы, которые могут быть использованы для дальнейшего исследования.

Конфирматорный факторный анализ

Конфирматорный факторный анализ проводится для подтверждения уже выработанных гипотез. Этот вид факторного анализа  имеет строгие показатели и строгие критерии. Он предполагает, что уже выявлено какое-то количество факторов, необходимых для исследования и служит инструментом для проверки правильности выработанных гипотез, подтверждения выбранной структуры.  Изучаемые факторы тщательно продумываются и подбираются.

Исследователями в основном используется эксплораторный факторный анализ.

Бююль, А. SPSS: Искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей /А. Бююль, П. Цефель.– СПб: Диасофт.– СПб, 2001.– 608 с.
Дубров, А.М. Многомерные статистические методы для экономистов и инженеров /А.М. Дубров, В.С. Мхитарян, Л.И. Трошин /Учебн. для студ. эконом. специальностей ВУЗов.– М.: Финансы и статистика, 2000.
Дюк, В. Обработка данных на ПК в примерах / В. Дюк.– СПб: Питер, 1997. – 240 с.
Зациорский, В.М. Кибернетика, математика, спорт / В.М. Зациорский.– М.: Физкультура и спорт, 1969.–197 с.
Зациорский В

Осторожно: статистика! / В. Зациорский //Теория и практика физической культуры, 1989.– № 2.–С

52-55.
Ким, Дж.-О. Факторный анализ: статистические методы и практические вопросы / Дж.- О. Ким, Ч.У. Мьюллер // Факторный, дискриминантный и кластерный анализ / Пер.с англ. – М.: Финансы и статистика, 1989.– С. 5–74.
Масальгин, Н.А. Многомерный статистический анализ в исследованиях по физиологии спорта // Метод. разработка для аспирантов, преподавателей и слушателей Высшей школы тренеров и факультета усовершенствования / Н.А. Масальгин, А.С. Медведев.– М., 1991.– 35 с.
Самсонова, А.В. Факторный анализ. Направления применения и неиспользованные возможности /А.В. Самсонова //Вестник Балтийской Педагогической Академии.- 2005.- вып. 62.- С. 67-75
Самсонова, А.В. Факторный анализ в педагогических исследованиях в области физической культуры и спорта: учеб. пособие / А.В. Самсонова, И.Э. Барникова; Национальный государственный университет физической культуры, спорта и здоровья им. П.Ф. Лесгафта, Санкт-Петербург.– СПб.: , 2013. — 90 с.

Мастер настройки

• Критерий значимости факторов:
  • По собственному значению — отбираются только факторы с собственными значениями равными или большими 1. Считается, что те факторы, у которых этот показатель меньше 1, не вносят значительного вклада в объяснение результата.
  • По дисперсии — факторы отбираются по доле объясняемой дисперсии. В этом случае выбирают столько факторов, чтобы в сумме они объясняли не менее 70-75% дисперсии. В отдельных вариантах порог дисперсии может достигать 85-90%.
  • Задать число факторов — количество значимых факторов выбирается аналитиком самостоятельно.

Значение каждого критерия можно задать в специальном поле справа от соответствующей ему радиокнопки.

• Метод получения окончательного решения
  • Без вращения — исходные факторы, полученные методом главных компонент, остаются без изменений.
  • Варимакс — критерием является упрощение описания каждого фактора. В результате максимизируется нагрузка на каждый фактор относительно небольшого числа переменных, а факторные нагрузки остальных переменных минимизируются. Рекомендуется выбирать, когда требуется обеспечить высокую интерпретируемость результатов факторного анализа.
  • Квартимакс — данный критерий упрощает описание каждой переменной, то есть уменьшает число факторов, связанных с этой переменной.
• Ограничить число выходных факторов — необязательный флаг, при активации которого можно задать ограничивающее число выходных факторов в соответствующем поле области.

2. Методы, основанные на критерии автоинформативности системы признаков

Формальные алгоритмы рассматриваемой группы методов непосредственно не оперируют обучающей информацией о требуемом значении диагностируемой переменной. В то же время эта информация в неявном виде всегда присутствует в экспериментальных данных. Она закладывается на самом первом этапе конструирования психодиагностического теста, когда экспериментатор формирует исходное множество признаков, каждый из которых, по его мнению, должен отражать определенные аспекты тестируемого свойства. При этом под отражением данного свойства отдельным признаком, как правило, понимается самый простой вид связи признака с диагностируемым показателем — корреляция xi с у. Если тестируемое свойство гомогенно, то имеются все основания полагать, что мерой информативности для окончательного отбора признаков может служить степень согласованного действия этих признаков в нужном направлении.

Внутренняя согласованность заданий теста является важной категорией методов, опирающихся на критерий автоинформативности системы признаков. Согласованность измеряемых реакций испытуемых на тестовые стимулы означает то, что они должны иметь статистическую направленность на выражение общей, главной тенденции теста

Геометрическая структура экспериментальных данных, сформированных под влиянием кумулятивного эффекта согласованного взаимодействия признаков, в несколько идеализированном варианте выглядит как облако точек в пространстве признаков, вписывающееся в гиперэллипсоид. Все пары признаков при такой структуре имеют статистически значимые корреляции, а уравнение главной оси гиперэллипсоида — есть линейная диагностическая модель тестируемого свойства.

На приведенных представлениях базируются практически все методы построения психодиагностических тестов, опирающиеся на критерий автоинформативности системы признаков и использующие категорию внутренней согласованности заданий теста. Ниже будут рассмотрены основные методы этой группы.

Детерминированный факторный анализ

Для проведения детерминированного факторного анализа используют несколько моделей:

• кратную;
• адаптивную;
• мультипликативную.

В процессе осуществления вычислений при помощи каждой из них используют данные об исследуемых факторах, а также конечный результат.

Модель детерминированного факторного анализа	Формула	Расшифровка формулы
Кратная	А / А1	А, А1 – факторы
Адаптивная	А + А1 + А2 + … +Ан	А, А1, А2, Ан – факторы
Мультипликативная	А * А1 * А2 * … *Ан	А, А1, А2, Ан – факторы

То есть, детерминированный факторный анализ проводится путем нахождения частного от исследуемых факторов, их произведения или суммы.

Методы детерминированного факторного анализа

Детерминированный факторный анализ проводят при помощи следующих методов:

• цепных постановок;
• логарифмирования;
• абсолютных разниц;
• интегрального;
• относительных разниц.

Для получения достоверного результата, нужно тщательно отобрать факторы, которые непосредственно влияют на конечный результат деятельности.

Метод цепных постановок

Метод цепных подстановок представляет собой последовательную замену одного из показателей прошлого периода с отчетным. При этом все остальные факторы остаются нетронутыми. Изменяя показатель, необходимо проводить новый расчет.

Для анализа используют факторную модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Чтобы определить взаимосвязь между факторами и конечным результатом, необходимо найти разницу между результатами расчетов. Для этого из итога второго расчета нужно отнять результат первого, из третьего – второго, из четвертого – третьего и так далее

В процессе исследования важно соблюдать строгую последовательность, в противном случае, анализ может показать некорректную информацию

Метод логарифмирования

Метод логарифмирования считается одним из наиболее точных способов факторного анализа. Он заключается в составлении логарифма на основании показателей прошлого и отчетного периода.

Для этого находят сумму всех факторов, затем записывают алгебраическое выражение в виде произведения отношения фактических факторов к плановым. А уже на основании него составляют логарифм.

Метод абсолютных разниц

Основой для вычисления методом абсолютных разниц служит факторная модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Но для начала нужно найти абсолютные отклонения. Для этого из факторов базисного периода отнимают плановые показатели.

Для определения взаимосвязи между ними необходимо провести анализ при помощи факторной модели, заменяя относительные результаты на абсолютные отклонения.

Интегральный метод

Интегральный метод используется только тогда, когда конечный результат можно представить в виде функции от нескольких показателей. Интегральное выражение показывает зависимость функции от аргументов.

Метод относительных разниц

Метод относительных разниц используется для измерения влияния факторов на динамику конечного результата в мультипликативных и смешанных моделях. Он применяется в том случае, если данные для расчета выражены в относительных отклонения факторных показателей (процентах).

При проведении анализа данным методом за основу берется факторная модель:

ФМ = А * Б * В…Я,

где А, Б, В…Я – показатели, используемые в процессе.

Относительные отклонения находят по формуле:

(Аф – Ап) / Ап,

где Аф – фактический показатель;

Ап – плановый или базисный показатель.

Оценка экономического рейтинга

Экономические параметры играют важную роль в определении экономического роста в целом, а также оказывают влияние на отдельные показатели, касающиеся здоровья экономики той или иной страны. В связи с активным техническим прогрессом и глобальным развитием цивилизации, конкуренция между странами во всех отношениях только усиливается.

И если проводить пофакторный анализ конкурентоспособности стран по уровням экономического развития для всесторонней, объективной и систематической оценки, необходимо учитывать каждый признак, отражающий определённую информацию об экономике с разных точек зрения. Но стоит понимать, что между различными примерами параметров существуют некоторые взаимосвязи, иначе отражённая информация будет генерировать дублирующие друг друга результаты, А это может привести к искажению реальной картины о состоянии экономики конкретной страны.

Чтобы проводить результативные исследования с использованием методов пофакторного анализа в экономике, нужно с особой тщательностью подходить к подбору параметров. В случае определения экономического рейтинга стран оптимальным считается следующий выбор исходных данных:

1. Валовой внутренний продукт на душу населения в текущих ценах (национальная валюта).
2. Коэффициент конверсии (в национальной валюте на текущий международный доллар).
3. Общий объём инвестиций (в процентах от ВВП).
4. Валовые национальные сбережения (в процентах от ВВП).
5. Объём импорта товаров (изменение в процентах).
6. Объём экспорта товаров (изменение в процентах).
7. Уровень безработицы (в процентах от общего количества рабочей силы).
8. Занятость (количество человек).
9. Население (количество).
10. Доходы органов управления (национальная валюта).
11. Общие расходы этих органов.
12. Чистые кредиты и займы сектора государственного управления.
13. Структурный баланс органов государственного управления (национальная валюта).
14. Валовой государственный долг (национальная валюта).
15. Валютный баланс (доллары США).

Метод главных компонент

Метод главных компонент (МГК) был предложен Пирсоном в 1901 году и затем вновь открыт и детально разработан Хоттелингом
/1933/. Ему посвящено большое количество исследований, и он широко представлен в
литературных источниках, обратившись к которым можно получить сведения о методе
главных компонент с различной степенью детализации и математической строгости (например, Айвазян С. А. и др., 1974, 1983, 1989). В данном разделе не ставится цель добиться подробного изложения всех особенностей МГК

Сконцентрируем свое внимание на основных феноменах
метода главных компонент

Метод главных компонент осуществляет переход к новой системе координат y₁,…,у_р в исходном пространстве признаков x₁,…,x_p которая является системой ортнормированных линейных комбинаций

где m_i — математическое ожидание признака x_i. Линейные комбинации выбираются таким образом, что среди всех возможных линейных нормированных комбинаций исходных признаков первая главная компонента у₁(х) обладает наибольшей дисперсией. Геометрически это выглядит как ориентация новой координатной оси у₁ вдоль направления наибольшей вытянутости эллипсоида рассеивания объектов исследуемой выборки в пространстве признаков x₁,…,x_p. Вторая главная компонента имеет наибольшую дисперсию среди всех оставшихся линейных преобразований, некоррелированных с первой главной компонентой. Она интерпретируется как направление наибольшей вытянутости эллипсоида рассеивания, перпендикулярное первой главной компоненте. Следующие главные компоненты определяются по аналогичной схеме.

Вычисление коэффициентов главных компонент w_ij основано на том факте, что векторы w_i= (w₁₁,…,w_pl)’, … , w_p = (w_1p, … ,w_pp)’ являются собственными (характеристическими) векторами корреляционной матрицы S. В свою очередь, соответствующие собственные числа этой матрицы равны дисперсиям проекций множества объектов на оси главных компонент.

Алгоритмы, обеспечивающие выполнение метода главных компонент, входят практически во все пакеты статистических программ.

4.1. Метод цепных подстановок

Метод цепных подстановок заключается в определении ряда промежуточных значений результативного показателя путем последовательной замены базисных значений факторов на отчетные. Данный способ основан на элиминировании. Элиминировать — значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Предполагается, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения, потом изменяются два при неизменности остальных и т.д.

В общем виде применение способа цепных постановок можно описать следующим образом:

где a, b, c — базисные значения факторов, оказывающих влияние на обобщающий показатель у;a₁ , b₁, c₁ — фактические значения факторов;y_a, y_b, — промежуточные изменения результирующего показателя, связанного с изменением факторов а, b соответственно.

Общее изменение Δу = у₁ — у складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

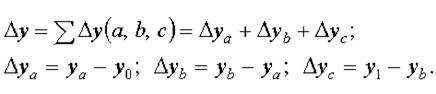
Рассмотрим пример. Исходные данные для факторного анализа сведены в таблицу 4.1. На основе этих данных проведем описанным выше способом анализ влияния на объем товарной продукции количества работников и их выработки.

Таблица 4.1

Исходные данные для факторного анализа

Показатели	Услов. обозн-я	Базисные значения (0)	Фактические значения (1)	Изменение
Абсолютное (+,- )	Относительное (%)
Объем товарной продукции, тыс. руб.	ТП	2920	3400	+480	116,40
Количество работников, чел	Ч	20	25	+5	125,00
Выработка на одного работающего, тыс. руб.	СВ	146	136	-10	93,15

Зависимость объема товарной продукции от данных факторов можно описать с помощью мультипликативной модели:

ТП  = Ч — СВ,

ТП  =  Ч · CB = 20 — 146 = 2920 (тыс. руб.).

Тогда   влияние   изменения   величины   количества   работников на обобщающий показатель можно рассчитать по формуле:

ТПусл₁ = Ч₁ — СВ = 25 — 146 = 3650 (тыс. руб.),

ΔТПусл₁ = ТПусл₁ — ТП0 = 3650 — 2920 = 730 (тыс. руб.).

Далее   определим   влияние   изменения   выработки   работников на обобщающий показатель:

ТП₁ = Ч₁ · СВ₁  =  25 · 136  =  3400 (тыс. руб.)

ΔТПусл₂ = ТП₁ — ТПусл₁ = 3400 — 3650 = — 250 (тыс. руб.)

Таким образом, на увеличение объема товарной продукции на 730 тыс. руб. положительное влияние оказало изменение на 5 человек численности работников. Отрицательное влияние оказало снижение выработки на 10 тыс. руб., что вызвало снижение объема на 250 тыс. руб. Суммарное влияние двух факторов привело к увеличению объема продукции на 480 тыс. руб.

Преимущества данного способа: универсальность применения, простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки:

• при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов;
• если модель представлена несколькими количественными и качественными показателями, то в первую очередь определяется влияние факторов первого порядка, затем второго и т.д.

Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.).

Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, средняя продолжительность рабочего дня и т.д.).

Понятие, задачи и типы факторного анализа

Все явления и процессы хозяйственной деятельности предприятий находятся во взаимосвязи. Одни из них непосредственно связаны между собой, другие  — косвенно. Каждое явление можно рассматривать как причину и как следствие.

Под факторным анализом понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.

Различают следующие типы факторного анализа: детерминированный и стохастический; прямой и обратный; одноступенчатый и многоступенчатый; статический и динамический; ретроспективный (исторический) и перспективный (прогнозный) .

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. когда результативный показатель представлен в виде произведения, частного или алгебраической суммы факторов.

Стохастический анализ представляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при стохастической связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель. Например, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания других факторов, воздействующих на этот показатель.

При прямом факторном анализе исследование ведется дедуктивным способом — от общего к частному. Обратный факторный анализ осуществляет исследование причинно-следственных связей способом логичной индукции — от частных, отдельных факторов к обобщающим. Факторный анализ может быть одноступенчатым и многоступенчатым. Первый тип используется для исследования факторов только одного уровня (одной ступени) подчинения без их детализации на составные части. При многоступенчатом факторном анализе проводится детализация факторов a и b на составные элементы с целью изучения их поведения. Детализация факторов может быть продолжена и дальше.

Необходимо различать также статический и динамический факторный анализ. Первый вид применяется при изучении влияния факторов на результативные показатели на соответствующую дату. Другой вид представляет собой методику исследования причинно-следственных связей в динамике.

Факторный анализ может быть ретроспективным, который изучает причины изменения результативных показателей за прошлые периоды, и перспективным, который исследует поведение факторов и результативных показателей в перспективе.

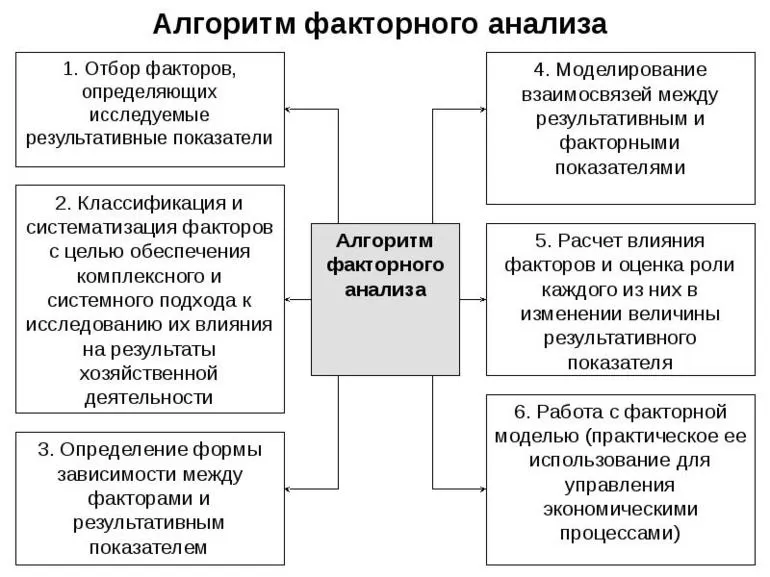
1. Отбор факторов для анализа исследуемых результативных показателей.

2. Классификация и систематизация факторов с целью обеспечения комплексного и системного подхода к исследованию их влияния на результаты хозяйственной деятельности.

3. Определение формы зависимости и моделирование взаимосвязей между факторными и результативными показателями.

4. Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя.

5. Работа с факторной моделью (практическое ее использование для управления экономическими процессами) .

Отбор факторов для анализа того или другого показателя осуществляется на основе теоретических и практических знаний, приобретенных в этой отрасли. При этом обычно исходят из принципа: чем больший комплекс факторов исследуется, тем точнее будут результаты анализа.

Самый главный методологический аспект в АХД — расчет влияния факторов на величину результативных показателей, для чего в анализе используется целый арсенал способов, сущность, назначение, сфера применения которых и процедура расчетов рассматриваются в следующих главах. И наконец, последний этап факторного анализа — практическое использование факторной модели для подсчета резервов прироста результативного показателя, для планирования и прогнозирования его величины при изменении производственной ситуации.

Литература:

1. Савицкая, Г. В. Анализ хозяйственной деятельности предприятий АПК: Учеб. пособие. — 4-е изд., испр. и доп. —  Мн.: Новое знание, 2004. — 736 с.

2. Савицкая, Г. В. Анализ хозяйственной деятельности предприятий АПК: Учеб. пособие. — 6-е изд., стер. – Мн.: Новое знание, 2006. — 652 с.

ФАКТОРНЫЙ АНАЛИЗ: ОБЩАЯ ХАРАКТЕРИСТИКА И СПОСОБЫ ПРОВЕДЕНИЯ

Факторный анализ — это способ комплексного и системного исследования влияния отдельных факторов на размер итоговых показателей. Основная цель проведения такого анализа — найти способы увеличить доходность фирмы.

Факторный анализ позволяет определить общее изменение прибыли в текущем периоде по отношению к предыдущему (базовому) периоду или изменение фактических показателей прибыли по отношению к плану, а также влияние на эти изменения следующих факторов:

• объем продажи продукции;
• себестоимость реализуемой продукции;
• цены реализации;
• ассортимент реализуемой продукции.

Таким образом, с помощью факторного анализа можно установить объем продаж, себестоимость или цену реализации, которые увеличат прибыль компании, а факторный анализ по ассортименту реализуемой продукции даст возможность выявить товар, который продается лучше всего, и товар, пользующийся наименьшим спросом.

Показатели для факторного анализа берут из бухгалтерского учета. Если анализируют итоги за год, то используют данные формы № 2 «Отчет о финансовых результатах».

Факторный анализ можно проводить:

1) способом абсолютных разниц;

2) способом цепных подстановок.

Математическая формула модели факторного анализа прибыли от продаж:

ПР = V_прод × (Ц – S_ед),

где ПР — прибыль от продаж (плановая или базовая);

V_прод — объем продаж продукции (товаров) в натуральных величинах (штуки, тонны, метры и т. д.);

Ц — продажная цена единицы реализованной продукции;

S_ед — себестоимость единицы реализованной продукции.

Способ абсолютных разниц

За основу факторного анализа берется математическая формула ПР (прибыль от продаж). Формула включает три анализируемых фактора:

• объем продаж в натуральных единицах;
• цену;
• себестоимость одной единицы продаж.

Рассмотрим ситуации, влияющие на прибыль. Определим изменение величины прибыли за счет каждого фактора. Расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей. Приведем формулы расчета для каждой ситуации, оказавшей влияние на прибыль.

Ситуация 1. Влияние на прибыль объема продаж:

ΔПР_объем = ΔV_прод × (Ц_план – S_{ед. план}) = (V_{прод. факт} – V_{прод. план}) × (Ц_план – S_{ед. план}).

Ситуация 2. Влияние на прибыль продажной цены:

ΔПР_цена = V_{прод. факт} × ΔЦ = V_{прод. факт} × (Ц_факт – Ц_план).

Ситуация 3. Влияние на прибыль себестоимости единицы продукции:

ΔПР_Sед = V_{прод. факт} × (–ΔS_ед) = V_{прод. факт} × (–(S_{ед. факт} – S_{ед. план})).

Способ цепной подстановки

Используя такой метод, сначала рассматривают влияние одного фактора при неизменности прочих, затем второго и т. д. За основу берут все ту же математическую формулу модели факторного анализа прибыли от продаж.

Выявим влияние факторов на сумму прибыли.

Ситуация 1. Изменение объема продаж.

ПР1 = V_{прод. факт} × (Ц_план – S_{ед. план});

ΔПР_объем = ПР1 – ПР_план.

Ситуация 2. Изменение цены продаж.

ПР2 = V_{прод. факт} × (Ц_факт – S_{ед. план});

ΔПР_цена = ПР2 – ПР1.

Ситуация 3. Изменение себестоимости продаж единицы продукции.

ПР_Sед = V_{прод. факт} × (Ц_факт – S_{ед. факт});

ΔПР_Sед = ПР3 – ПР2.

Условные обозначения, применяемые в приведенных формулах:

ПР_план — прибыль от реализации (плановая или базовая);

ПР1 — прибыль, полученная под влиянием фактора изменения объема продаж (ситуация 1);

ПР2 — прибыль, полученная под влиянием фактора изменения цены (ситуация 2);

ПР3 — прибыль, полученная под влиянием фактора изменения себестоимости продаж единицы продукции (ситуация 3);

ΔПР_объем — сумма отклонения прибыли при изменении объема продаж;

ΔПР_цена — сумма отклонения прибыли при изменении цены;

ΔП_Sед — сумма отклонения прибыли при изменении себестоимости единицы реализованной продукции;

ΔV_прод — разница между фактическим и плановым (базисным) объемом продаж;

ΔЦ — разница между фактической и плановой (базисной) ценой продаж;

ΔS_ед — разница между фактической и плановой (базисной) себестоимостью единицы реализованной продукции;

V_{прод. факт} — объем продаж фактический;

V_{прод. план} — объем продаж плановый;

Ц_план — цена плановая;

Ц_факт — цена фактическая;

S_{ед. план} — себестоимость единицы реализованной продукции плановая;

S_{ед. факт} — себестоимость единицы реализованной продукции фактическая.

Замечания

1. Способ цепной подстановки дает те же результаты, что и способ абсолютных разниц.
2. Суммарное отклонение прибыли будет равно сумме отклонений под влиянием всех факторов, по которым проводят факторный анализ.

Альтернативные стратегии оценки

Хотя для оценки моделей CFA использовались многочисленные алгоритмы, метод максимального правдоподобия (ML) остается основной процедурой оценки. При этом модели CFA часто применяются к условиям данных, которые отклоняются от нормальных теоретических требований для достоверной оценки ML. Например, социологи часто оценивают модели CFA с ненормальными данными и показателями, масштабируемыми с использованием дискретных упорядоченных категорий. Соответственно, были разработаны альтернативные алгоритмы, учитывающие различные условия данных, с которыми сталкиваются прикладные исследователи. Альтернативные оценки были охарактеризованы в два общих типа: (1) робастные и (2) ограниченные информации оценки.

Когда ML реализуется с данными, которые отклоняются от предположений нормальной теории, модели CFA могут давать смещенные оценки параметров и вводящие в заблуждение выводы. Робастная оценка обычно пытается исправить проблему путем корректировки нормальной теоретической модели χ 2 и стандартных ошибок. Например, Саторра и Бентлер (1994) рекомендовали использовать оценку машинного обучения обычным способом с последующим делением модели χ 2 на меру степени многомерного эксцесса. Дополнительным преимуществом надежных оценщиков машинного обучения является их доступность в общем программном обеспечении SEM (например, LAVAAN).

К сожалению, робастные оценщики машинного обучения могут оказаться непригодными в условиях обычных данных. В частности, когда показатели масштабируются с использованием нескольких категорий ответов (например, не согласен , нейтральный , согласен ), надежные оценщики машинного обучения, как правило, работают плохо. Оценщики с ограниченной информацией, такие как взвешенный метод наименьших квадратов (WLS), вероятно, являются лучшим выбором, когда явные индикаторы принимают порядковую форму. В целом, оценщики с ограниченной информацией обращаются к порядковым индикаторам, используя полихорические корреляции для соответствия моделям CFA. Полихорические корреляции отражают ковариацию между двумя скрытыми переменными, когда наблюдается только их категоризованная форма, что достигается в основном за счет оценки пороговых параметров.

Примеры расчетов

На практике аналитические расчеты проводят в виде таблицы, поскольку для получения результата необходимо установить влияние сразу нескольких факторов на исследуемый показатель. Сравнение проводят между предыдущим и текущим периодами, чтобы получить адекватную картину (рыночные цены не изменились или по крайней мере изменились незначительно).

Факторный анализ прибыли от продаж

параметр	прошлый период	исследуемый период	изменение прибыли
в абсолютных значениях	в относительных значениях, %
объем продаж	10000	10500	500	5,0
себестоимость единицы	500	450	-50	-10
чистая прибыль	1700	2000	300	17,6
коммерческие издержки	1400	1600	200	15,4
управленческие издержки	700	800	700	14,3
индекс изменения цен	2,00	2,20	0,20	10

Из этих данных можно сделать несколько выводов:

1. Объем продаж за отчетный период увеличился на 5%.
2. В том числе этому способствовало снижение себестоимости на 10%.
3. С другой стороны, выросли и издержки – на 15,4% коммерческие и на 14,3% управленческие.
4. Поэтому фактор снижения себестоимости на 10% не привел к аналогичному изменению дохода, который увеличился только на 5%.

Факторный анализ чистой прибыли

В этом случае за основу берут 3 показателя – это доход, себестоимость единицы и чистая прибыль.

параметр	объем продаж	абсолютная разница	относительная разница
прошлый период	исследуемый период
доход	70000	80000	10000	14,3%
себестоимость единицы	65000	67000	2000	3,1%
чистая прибыль	12000	13000	1000	8,3%

Из этого примера факторного анализа можно сделать несколько выводов:

1. Себестоимость единицы продукции увеличилась на 3,1%, что явилось негативным фактором.
2. Однако доход все равно увеличился на 14,3%.
3. Также увеличилась и чистая прибыль на 8,3%.

Поэтому подобный рост себестоимости оказался приемлемым. Следовательно, действуют другие факторы, которые позволяют расти прибыли компании. Уточнить их степень влияния можно с помощью аналогичных расчетов.