Показатели индекса доходности предприятия

Индексы рентабельности инвестиций

Во многих источниках целью инвестирования (вложения средств) является получение прибыли или дохода (чаще всего в виде выручки), но поскольку окупаемость инвестиций (инвестиционных проектов) возможна только при получении положительного экономического эффекта, то в дальнейшем целью инвестирования необходимо считать получение экономического эффекта. Достижение положительного экономического эффекта означает, что инвестиционные затраты окупились и приносят. Исходя из выше сказанного инвестиции – это денежные средства, вклады ценные бумаги, оборудование, технологии, любое другое имущество или имущественные и авторские права, вкладываемые в предпринимательскую или иную деятельность в целях получении положительного экономического эффекта. По этому, что бы оценить эффективность инвестиционного проекта, а об эффективности инвестиций можно судить по их доходности, нужно прибегать к финансово экономическому анализу.

Одним из аналитических инструментов, является индекс прибыльности инвестиций. Данный индекс имеет широкое применение при аналитическом анализе рынка, и показывает количество прибыли, которую мы получим за каждую вложенную единицу средств. В упрощённом варианте, индекс доходности можно представить как отношение суммы прибыли к абсолютной величине инвестиций, и рассчитывается путем деления текущей стоимости будущих прибылей от проекта к первоначальным инвестициям, необходимых для реализации проекта.

Формула, по которой можно сделать расчёт индекса рентабельности инвестиций РI,имеет следующий вид:

где

Bi – чистый денежный доход і–го года, руб;

n – количество периодов эксплуатации проекта, год;

I0 – первоначальные инвестиции проекта, руб.

r – ставка дисконтирования.

Или же формула индекса рентабельности инвестиций может иметь упрощённый вид:

где

NPV–чистая текущая стоимость;

PV–суммарный денежный доход от проекта (дисконтированный доход);

I0 – первоначальные инвестиции проекта, руб.

Если при реализации инвестиционного проекта, капитальные вложения осуществляются в несколько этапов, то индекс рентабельности инвестиций PI, будет рассчитываться по следующей формуле:

Индекс прибыльности инвестиций это относительный показатель, который характеризует уровень доходов на единицу затрат, то есть чем выше значения этого показателя тем вше уровень отдачи от инвестиционного капитала. Если индекс доходности инвестиций равен 1 то инвестиций не будут приносить прибыль также как и не будут убыточными, когда показатель доходности меньше 1 инвестиции будут убыточными, а при боле 1 будут приносить прибыль.

Показатель индекса доходности инвестиций может применяться как перед началом инвестирования, так и на каждой стадии, а также при возврате инвестиций. Использования индекса доходности, на разных этапах инвестирования, даёт возможность инвестору провести сравнение реальной доходности проекта с предполагаемыми ранее показателями. Также стоит отметить, что индекс рентабельности очень удобный при выборе одного проекта из нескольких альтернативных, что имеют приблизительно одинаковые показатели чистой текущей стоимости NPV, или при формировании инвестиционного портфеля или инвестиции в индексы, с максимальным суммарным NVP в условиях ограниченности денежных ресурсов.

Метод индекса рентабельности инвестиций имеет главный недостаток, им является его большая чувствительность к масштабу проекта. Он не всегда может дать оценку эффективности инвестиций, и может получиться так, что инвестиционный проект с самым большим РI. может не отвечать проекту, с наиболее высокой чистой текущей стоимостью NPV.

Доказательство перегруппировкой [ править | править код ]

Следуя Сато Мошуну и Леонардо да Винчи , мы можем использовать вписанные правильные многоугольники другим способом. Положим, мы вписали шестиугольник. Разрежем шестиугольник на шесть треугольников, делая сечения через центр. Два противоположных треугольника содержат общие диаметры. Сдвинем теперь треугольники, чтобы радиальные стороны стали смежными. Теперь пара треугольников образует параллелограмм, в котором стороны шестиугольника образуют две противоположные стороны длиной s. Две радиальные стороны становятся боковыми сторонами, а высота параллелограмма равна h (как в доказательстве Архимеда). Фактически, мы можем собрать все треугольники в один большой параллелограмм, располагая в ряд полученные параллелограммы (из двух треугольников). То же самое будет верно, если мы будем увеличивать число сторон. Для многоугольника с 2n сторонами параллелограмм будет иметь основание ns и высоту h. С ростом числа сторон длина основания параллелограмма увеличивается, стремясь к половине окружности, а высота стремится к радиусу. В пределе параллелограмм становится прямоугольником с шириной π r и высотой r.

n	сторона	основание	высота	площадь
4	1,4142136	2,8284271	0,7071068	2,0000000
6	1,0000000	3,0000000	0,8660254	2,5980762
8	0,7653669	3,0614675	0,9238795	2,8284271
10	0,6180340	3,0901699	0,9510565	2,9389263
12	0,5176381	3,1058285	0,9659258	3,0000000
14	0,4450419	3,1152931	0,9749279	3,0371862
16	0,3901806	3,1214452	0,9807853	3,0614675
96	0,0654382	3,1410320	0,9994646	3,1393502
∞	1/∞	π	1	π

Зачем это нужно инвестору

Инвестиция — это не волшебная палочка, которая постоянно будет приносить вам прибыль, и при этом ничего от вас не требовать

Важно, что учет должен быть постоянным, а вот контроль — нет. Проводить учет инвестиций может каждый, даже если в школе были большие проблемы с математикой, и вы никогда не помните, сколько у вас денег на карточках и в кошельке в виде кэша

Фактически, имеется 2 метода, с помощью которых каждая ваша инвестиция будет под четким контролем:

• В письменном виде — по старинке в блокноте на основе нескольких формул;
• С помощью специальных программ или элементарной офисной программы Excel, фирменных калькуляторов организаций или проектов.

Отмечу, что для удобства контроля каждой инвестиции и оценки ее рентабельности работает портфель инвестиций на GQ Blog Monitor, позволяющий детально и без лишних хлопот оценивать ситуацию и видеть, сколько вы заработали за конкретный период или с конкретным проектом. На момент подготовки материала услуги и простоту криптопортфеля ощутили на собственном опыте 460 инвесторов.

По своему опыту могу сказать, что это крайне удобно, поскольку в него подвязываются инвестиции с различных хайпов, плюс можно и учитывать работу на бирже криптовалют. А если вы новичок в этом финансовом направлении — материал на блоге поможет детально ознакомиться с тонкостями работы.

 
Не пускайте деньги на самотёк, но и не контролируйте каждую копейку. Деньги любят учет, но не любят страха. Причем не только фиат, но и криптовалюта.

Если вы ценитель классической работы с деньгами, тогда самое время пополнить свой массив знаний определенными формулами, помогающими рассчитать наперед — выгодно или не выгодно вкладываться в проект.

Дисконтированный индекс доходности

Еще один показатель, помогающий проанализировать рентабельность вложений. Его формула выглядит вот так:

Здесь:

• PV – общий доход
• IC – вложения на первом этапе

Это частный случай – здесь денежные средства вкладываются единовременно. В общем случае уравнение выглядит следующим образом:

Здесь:

• PVi – полная прибыль проекта за период i
• ICi – объем вложений в период i
• r – ставка дисконтирования
• n – количество итераций (сколько раз вы вкладывали деньги)

Главный недостаток метода – нельзя сравнивать финансовые потоки, относящиеся к разным периодам. В этом случае результаты не будут объективными.

Пример:

• Объем вложений – 100 000 рублей
• Доход от инвестиций в 1-й год: 30 000 рублей
• 2-й год: 41 000 рублей;
• 3-й год: 43 000 рублей;
• 4-й год: 38 000рублей;
• Барьерная ставка –а 10%.

Считаем доходы:

• PV1 = 30000 / (1 + 0,01) = 29 703
• PV2 = 41000 / (1 + 0,01) = 40 594
• PV3 = 43000 / (1 + 0,01) = 42 574
• PV4 = 38000 / (1 + 0,01) = 37 623
• DPI = (29703 + 40 594 + 42 574 + 37 623) / 100 000 = 1,50 – рентабельность проекта отличная.

Расчеты дисконтированного индекса прибыльности учитывают либо все капиталовложения за определенный период, либо инвестиции непосредственно перед запуском проекта. В этих случаях показатель DPI примет разные значения.

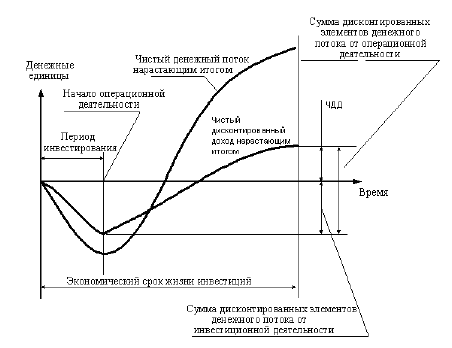
Доказательство Архимеда [ править | править код ]

Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.

Не больше

Предположим, что площадь круга C больше площади треугольника T = 1 ⁄₂cr. Пусть E означает превышение площади. Впишем квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G₄ больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G₈. Продолжаем деление, пока общий зазор G_n не станет меньше E. Теперь площадь вписанного многоугольника P_n = C − G_n должна быть больше площади треугольника.

G_\P_&<>=C-G_\&<>>C-E\P_&<>>Tend>>»> E = C − T > G n P n = C − G n > C − E P n > T <displaystyle <eginE&<>=C-T\&<>>G_\P_&<>=C-G_\&<>>C-E\P_&<>>Tend>> G_\P_&<>=C-G_\&<>>C-E\P_&<>>Tend>»/>

Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1 ⁄₂nhs. Но h 1 ⁄₂cr, получили противоречие.

Не меньше

Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G₄ больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника P_n должна быть меньше T.

G_\P_&<>=C+G_\&<> D = T − C > G n P n = C + G n C + D P n T <displaystyle <eginD&<>=T-C\&<>>G_\P_&<>=C+G_\&<> G_\P_&<>=C+G_\&<>

Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.

Таким образом, площадь круга в точности равна площади треугольника.

Индекс рентабельности PI как индикатор рентабельности

Далее, переходим к анализу еще одного распространенного индикатора – индекса рентабельности инвестиций PI (Profitability Index). Для контроля рентабельности проекта, инвестор должен проводить анализ PI на всех этапах инвестирования: в момент выбора объекта, сравнения с альтернативами, реализации и завершения. Если значение индекса больше 1, проект считается прибыльным. Если меньше 1 – убыточным. Если же индекс равен единице, необходимо провести более тщательный анализ прочих факторов рентабельности.

Определяется PI так:

PI = NPV/IC

NPV (Net Present Value) – чистая текущая стоимость инвестиций. Из русскоязычных аналогов NPV чаще всего встречается аббревиатура ЧДД – чистый дисконтированный доход. IC – инвестиции в проект (Invested Capital).

Теперь нам осталось рассчитать NPV (ЧДД), значение которого, для окупаемости проекта, должно быть выше или как минимум равно нулю.

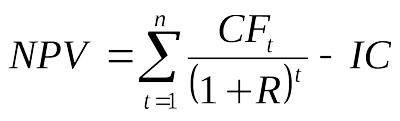
CFt – денежный поток (Cash Flow) в t-м году;

N – длительность жизненного цикла проекта (в месяцах, годах);

R – от слова Rate, ставка или норма дисконтирования.

Ставка дисконтирования — это цена в процентных пунктах, которую инвестор готов заплатить за издержки и риски проекта. Эту ставку можно назвать также стоимостью фондирования инвестиций. Она может иметь в своей основе только ставку по кредиту, но стоит предусмотреть и иные издержки: валютные и политические риски, человеческий фактор при реализации бизнес-плана и др. В любом случае, планируемая инвестором доходность проекта должна быть выше ставки дисконтирования, а дисконтированный денежный поток суммарно должен быть больше вложенных инвестиций вместе с затратами.

В качестве примера, попробуем подставить в формулу реальные данные. Допустим, вы инвестировали 300$ на 3 года. Банковский кредит обошёлся вам в 13% годовых (не рекомендую вкладывать кредитные деньги). Поскольку других затрат на привлечение средств у вас не было, мы условно приравняем это к ставке дисконтирования. Денежный поток прогнозируем, исходя из статистики аналогичных проектов и учитывая максимально возможное число факторов (риски, издержки, инфляция и т.п.). В первую очередь вычисляем коэффициент дисконтирования вложенной суммы, для каждого года инвестиционного цикла, по формуле 1 (1+R)t. В момент инвестирования 300$ мы имеет коэффициент дисконтирования, равный единице. По результатам первого года получаем коэффициент 1 (1+R)1 = 0.885, для второго года 1 (1+R)2 = 0.783, для третьего — 1 (1+R)3 = 0.693. Переводим инвестиционный план в таблицу:

Год	Cash Flow	Коэффициент дисконтирования	Дисконтированный денежный поток
	-300	1	-300
1	110	0.885	97,35
2	135	0.783	105,71
3	156	0.693	108,11
ЧДД			11,17

Проект пригоден к реализации, так как NPV положительный. Делаем вывод, что чем выше ставка дисконтирования, тем ниже NPV. Индекс PI удобен при выборе из ряда альтернативных проектов того, что обеспечит наибольшую эффективность вложений. Он позволяет ранжировать проекты, имеющие схожие значения NPV. В отличие от коэффициента ROI, он учитывает риски, через применение ставки дисконтирования, а также оценивать будущие денежные потоки, с помощью коэффициента дисконтирования. Данный инструмент пригоден как для составления бизнес-плана, так и для выбора прибыльного объекта инвестирования. Недостатком PI можно назвать сложность прогнозирования ставки дисконтирования, которая иногда зависит от неконтролируемых факторов: стоимость заемных ресурсов, цена на нефть, курсы валют, санкции.

Также в рамках формулы PI непросто спланировать будущие денежные потоки, которые могут сократиться в будущем по объективным причинам. Неточность в расчетах естественным образом возрастает при больших сроках инвестирования. Здесь полезно отметить, что в российской практике инвестирования, оценка NPV показывает, что окупаемость вложений не должна превышать 3-4 лет в зависимости от рисков. Для банковского потребительского кредитования максимальный цикл возврата инвестиций может достигать пяти лет. Это связано с большой волатильностью валютных курсов и ключевой ставки. Все это негативно влияет на прогнозируемость ставки дисконтирования и денежного потока. Если же говорить о зарубежных активах, то в развитых странах положительный индекс PI планируется на горизонте от 7 лет и более.

P.S.

Попробуйте просчитать рентабельность своих инвестиционных проектов с использованием ROI и PI. Как всегда, приглашаю читателей блога оставить свои комментарии по теме. Возможны у вас есть чем дополнить статью.

Всем рентабельных инвестиций!

01.06.2017

Понятие рентабельности или индекса доходности

Рентабельность проекта обозначает его прибыльность. С помощью этого показателя оценивают потенциальную доходность любого бизнеса. На практике понятие рентабельности широко применяют для оценки экономического состояния предприятия, конкурентоспособности выпускаемой продукции или оказываемых услуг. Для этого отдельный вид продукции сравнивают с таковым у конкурирующих компаний или с другим видом товара, выпускаемого предприятием.

Этот индекс, как показатель, является универсальным. С его помощью можно сравнивать эффективность и прибыльность проектов различного масштаба. Если выразить индекс как понятие в числах, оно отобразит цифру чистой прибыли, делённую на количество затраченных ресурсов. Поэтому возникло понятие — рентабельности вложенного капитала или, простыми словами, доходности.

Как рассчитать индекс доходности

Метод определения рентабельности инвестиции (PI) проекта вкратце описан выше. Посчитать этот показатель можно по формуле:

Где:

• PI – индекс доходности инвестиций;
• NPV – сумма чистого дисконтированного дохода (с учетом ставки налога на прибыль);
• CI – величина вложенного капитала.

Как видно из математического выражения, индекс представляет безразмерный коэффициент: числитель и знаменатель — оба выражены в денежных единицах, которые взаимно сокращаются.

В некоторых случаях для удобства и наглядности PI измеряется в процентах. Для этого значение следует умножить на 100%.

Чтобы дисконтировать (привести к актуальным условиям) доход, следует воспользоваться еще одной формулой:

Где:

• NPV – сумма чистого дисконтированного дохода;
• i – номер периода реализации проекта (года или месяца);
• N – общая продолжительность реализации проекта (в годах или месяцах);
• Pi – сумма прибыли за отдельный период под номером i, называемая входящим отдельным денежным потоком;
• R – дисконтная ставка.

Значение R устанавливается инвестором и является его внутренней нормой. В некоторых случаях оно равно ставке рефинансирования Центрального банка РФ, но чаще превышает ее. Дело в том, что у крупного предпринимателя есть альтернативные варианты вложений, обеспечивающие ему определенную отдачу. Отвлекая средства на менее рентабельные направления, бизнесмен несет потери.

После простой подстановки, формула PI приобретает окончательный вид:

Теперь можно рассмотреть пример расчета.

Исходные данные:

• Сумма инвестиций в проект CI – 2 млн руб.
• Продолжительность реализации проекта N – 3 года.
• Прибыль за первый год – 120 тыс. руб.
• Прибыль за второй год – 1,3 млн руб.
• Прибыль за третий год – 2,2 млн руб.
• Дисконтная ставка – 18%.

После подстановки значений получается результат:

Из полученной итоговой суммы дисконтированного дохода (в числителе формулы) можно сделать вывод о том, что она больше вложенного капитала, а значение PI указывает, во сколько раз.

Очевидно, что за трехлетний период времени инвестору вернутся деньги, превышающие сумму вложений на 18,7%.

Оценка инвестиционного проекта в Excel

Рассчитывают 4 основных показателя:

• чистый приведенный эффект (ЧПЭ, NPV);
• индекс рентабельности инвестиций (ИРИ, PI);
• внутреннюю норму доходности (ВНД, IRR);
• дисконтированный срок окупаемости (ДСО, DPP).

Для примера возьмем следующий вариант инвестиций:

Сначала дисконтируем каждый положительный элемент денежного потока.

Создадим новый столбец. Введем формулу вида: = положительный элемент денежного потока / (1 + ставка дисконтирования)^ степень, равная периоду.

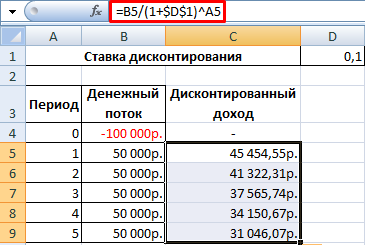
Теперь рассчитаем чистый приведенный эффект:

1. С помощью функции СУММ.
2. С помощью встроенной функции ЧПС.
   Чтобы получить чистый приведенный эффект, складываем результат функции с суммой инвестиций.
   Цифры совпали:

Найдем индекс рентабельности инвестиций. Для этого нужно разделить чистую приведенную стоимость (ЧПС) на объем инвестированных средств (со знаком «+»):

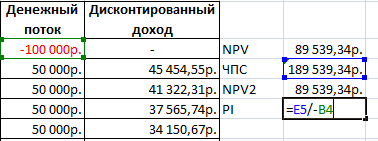
Посчитаем IRR инвестиционного проекта в Excel. Напомним формулу:

ВНД = ΣДП_t/ (1 + ВНР) t = И.

ДП_t– положительные элементы денежного потока, которые нужно продисконтировать по такой ставке, чтобы чистый приведенный эффект равнялся нулю. Внутренняя норма доходности – такая ставка дисконтирования, при которой выпадает равенство вида:

ΣДП_t / (1 + ВНР) t – И = 0,

Воспользуемся инструментом «Анализ «Что-Если»»:

1. Ставим курсор в ячейку со значением чистого приведенного эффекта. Выбираем «Данные»-«Анализ Что-Если»-«Подбор параметра».
2. В открывшемся окне в строке «Значение» вводим 0 (чистый приведенный эффект должен равняться 0). В поле «Изменяя значение ячейки» ссылаемся на ставку дисконтирования. Нужно изменить ее так, чтобы соблюдалось приведенное выше равенство.
3. Нажимаем ОК.

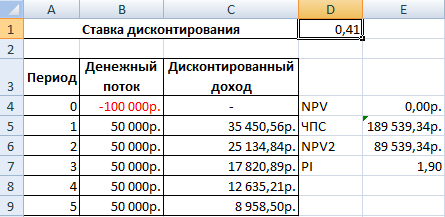
Ставка дисконтирования равняется 0,41. Следовательно, внутренняя норма доходности составила 41%.

Особенности расчёта доходности инвестиций в ПАММ-счета

Начнем с самого очевидного — графики доходности ПАММ-счетов у всех брокеров не соответствуют реальной доходности инвестора! То что мы видим — доходность именно ПАММ-счёта, то есть всей суммы инвестиций, включая и деньги управляющего, и комиссию за управление.

Когда мы видим такие цифры:

600% за полтора года, рука сразу же тянется к кнопке «Инвестировать», золотая жила же! Однако если мы учтем 29% комиссии управляющего, то реальная доходность окажется такой:

В 2 раза меньше! Я не спорю, 300% за полтора года тоже смотрятся отлично, но это далеко не 600%.

Ну а если углубиться в суть, то доходность ПАММ-счёта считается так:

• Общая доходность считается по формуле доходности за несколько периодов с реинвестированием.
• Положительный результат уменьшается на процент комиссии управляющего, кроме случаев в п.4 и 5.
• Отрицательный результат всегда остается как есть.
• Если положительный результат получен после убытка, он не уменьшается из-за комиссии, пока общая доходность не обновит максимум.
• Если после положительного результата превышен максимум общей доходности — комиссия снимается только с той части, которая превысила максимум.

В итоге получаем весьма замороченную формулу, которая необходима для высокой точности расчётов. Что делать, если вам нужно посчитать чистую доходность инвестора ПАММ-счёта? Предлагаю использовать такой алгоритм:

1. Общая доходность считается по формуле доходности за несколько периодов с реинвестированием.
2. Положительный результат уменьшается на процент комиссии управляющего.
3. Отрицательный результат уменьшается на процент комиссии управляющего.

Все что нужно — умножить официальные цифры доходности ПАММ-счёта на единицу минус комиссия управляющего. Причем не итоговый результат, а данные с графика ПАММ-счёта (в Альпари их можно скачать в удобном виде) и посчитать по формуле доходности за несколько периодов.

Для наглядности посмотрите на один и тот же график доходности, посчитанный тремя способами:

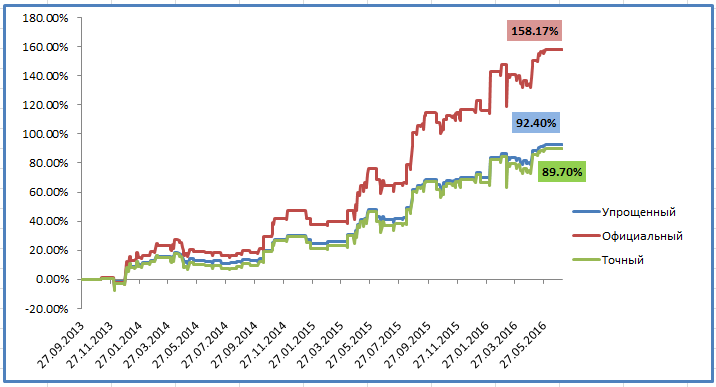
Разница с учётом и без учёта комиссии управляющего — почти в 2 раза! По упрощенному алгоритму мы получили результат 92%, по точному — 89%. Разница не существенная, но для тысяч процентов она станет вполне заметной:

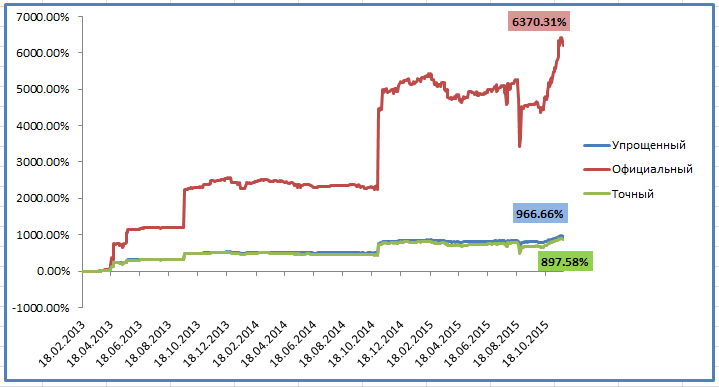
Реальная доходность инвестора ниже в 6 раз, а разница между точным и упрощенным алгоритмом 70% — на больших цифрах всё заметнее.

Кстати, вы хотите знать, откуда вообще берется эта разница? Кроме того, что упрощенный способ подсчета доходности уменьшает размер просадок, есть еще одна фишка — регулярные выплаты вознаграждения управляющего уменьшают вашу долю в ПАММ-счёте.

Вы все поймете, взглянув на эту картинку:

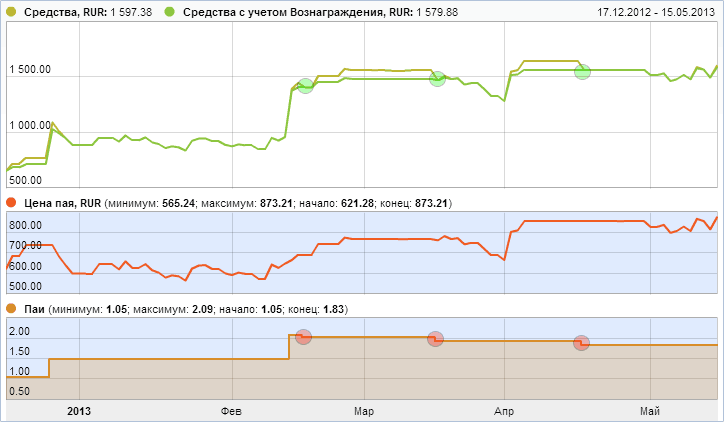
Зелеными кружками показаны моменты выплаты вознаграждения управляющего, красными — уменьшение ваших паёв в ПАММ-счёте. Что такое пай? Это ваша доля в ПАММ-счёте, ваш кусочек общего пирога прибыли.

Для понимания подойдет такое сравнение — паи это определенное количество акций ПАММ-счёта. По этим акциям вы получаете дивиденды — процент от прибыли компании. Количество акций уменьшается — снижаются дивиденды, соответственно и доходность вложений.

Почему же паи уменьшаются? Дело в том, что изначально вы получаете прибыль на всю сумму своих инвестиций — как и должны. Наступает момент выплаты комиссии управляющего — и она берется из вашей суммы, вашего «кусочка пирога». Кусочек стал меньше со всеми вытекающими.

То, что я вам показал — это не плохо, это как есть. Так работают ПАММ-счета, а вкладывать деньги или нет — выбор всегда за вами.

Ну и пожелание напоследок: инвестируйте в действительно доходные проекты!

Нормативное значение

Как таковой установленной нормы индекса доходности не существует

Важно лишь то, чтобы его значение было больше единицы. Это будет говорить о рентабельности проекта

Чем выше значение индекса, тем рентабельнее инвестиция. В том случае, когда индекс доходности ниже единицы, необходимо закрыть проект, поскольку инвестированные средства не возвращаются. В ситуации, когда ИД = 1, инвестор не получает ни прибыли, ни убытков.

Для наглядности стоит рассмотреть пример.

Длительность инвестиционного проекта составляет три года. Калькуляционный процент – 6%. Размер инвестиции – 10 тысяч рублей. В первый год проект приносит 3500 рулей, во второй и третий года – 4 тысячи рублей.

Первый шаг заключается в расчете чистой текущей стоимости проекта без учета инвестиций в период Т.

ЧТС = 3500 : 1,06 + 3500 : 1,062 + 3500 : 1,063 = 10 220,3 рублей.

Далее рассчитаем индекс доходности:

ИД = 10 220,3 : 10 000 = 1,02203.

Итак, индекс доходности больше единицы, это свидетельствует о целесообразности инвестиционного проекта.

Если бы, к примеру, во второй год размер поступлений составил бы 3500 рублей, то чистая приведенная стоимость была бы равна 9775,3 рублей. В этом случае проект не был бы эффективным, поскольку индекс доходности был бы равен 0,977, т. е. ниже единицы.

Что такое индекс рентабельности инвестиций

Для начала дадим определение индекса рентабельности инвестиций (PI).

PI — это параметр инвестиционного анализа, который позволяет провести оценку рентабельности инвестиционного проекта и его эффективности. Аббревиатура PI — это сокращенная версия англоязычного названия данного индекса — Profitability Index.

Индекс рентабельности является относительным показателем, который выражается в виде коэффициента. В экономическом анализе значение этого параметра заключается в том, что дает возможность спрогнозировать приведенную стоимость от реализации бизнес-проекта, которая будет получена в расчете на одну условную единицу первоначальных вложений.

Таким образом, индекс PI позволяет наиболее показательно оценить эффективность проекта. Можно посмотреть сколько прибыли приносит каждый рубль вложенных средств.

Поэтому данный показатель является наиболее важным при бизнес-планировании. Для того, чтобы понять, как правильно встроить определение индекса рентабельности инвестиций и других сопутствующих ему параметров, советуем вам ориентироваться на уже готовые образцы таких документов. Логичная структура таких документов позволит вам последовательно осуществить все шаги по бизнес-планированию будущего проекта.

В каких формулах используется число

Площадь круга радиуса $r : S=\pi r^{2}$

Длина окружности радиуса $r : l=2 \pi r$

Площадь сектора с угловой величиной дуги $\alpha^{\circ} : S_{\operatorname{сект}}=\frac{\pi r^{2} \alpha}{360}$

Объем цилиндра: $V=\pi R^{2} H$

Площадь боковой и полной поверхности цилиндра:

$S_{бок}=2 \pi R H$   и  $S_{цил}=2 \pi R H+2 \pi R^{2}$

Объем конуса: $V_{кон}=\frac{\pi R^{2} H}{3}$

Площадь боковой поверхности конуса: $S_{бок}=\pi R L$

Площадь сферы: $S=4 \pi R^{2}$

Объем шара: $V=\frac{4}{3} \pi R^{3}$

Пример

Задание. Вычислить объем и полную площадь поверхности цилиндра, если радиус основания цилиндра
$R=2$ см, а высота цилиндра $H=5$ см .

Решение. Объем цилиндра найдем по формуле

$$V=\pi R^{2} H$$

полагая $\pi=3,14$ и подставляя заданные значения, получим

$V=3,14 \cdot 2^{2} \cdot 5=3,14 \cdot 4 \cdot 5=62,8$ (см3)

Для нахождения полной площади поверхности цилиндра воспользуемся формулой

$$S_{цил}=2 \pi R H+2 \pi R^{2}$$

подставляя заданные значения, имеем

$S_{цил}=2 \cdot 3,14 \cdot 2 \cdot 5+2 \cdot 3,14 \cdot 2^{2}=87,59$ (см2)

Ответ. $V=62,8$ (см3)

            $S_{цил}=87,59$ (см2)

Читать дальше: что такое действительное число.

Определение и виды индексов доходности PI

Индекс доходности PI – ключевой индикатор, который используется для оценки перспективности инвестиционного проекта, с точки зрения его потенциальной доходности. В экономическом и финансовом анализе относится к главным и объективным критериям выбора и сравнительной оценки бизнес проектов.

Чтобы понять, что оценивает показатель, следует сначала дать определение самим инвестиционным процессам: это операции, в рамках которых капитал вкладывается в проект или компанию, с целью его возврата через заданный период времени, с определенной нормой рентабельности или прибыльности. Капитал – это не только денежные ресурсы, к нему относят:

• технологии;
• авторские права;
• патенты и другие понятия из сферы интеллектуальной собственности.

Проблема выбора конкретного проекта решается при помощи соответствующих индикаторов, позволяющих оценить привлекательность предложенных вариантов вложения ресурсов. К ним и относится индекс доходности PI, который позволяет рассчитать, сколько получит инвестор с каждого вложенного в проект рубля, то есть он отражает отношение прибыли к общему объему инвестиций в проект.

Используемые в английском языке названия и обозначение индекса доходности PI (индекса рентабельности):

• Profitability Index;
• Benefit cost ratio$
• DPI;
• Present value index».

В расчете индекса принимает участие два основных параметра – дисконтированная прибыль и общая величина инвестиционных вливаний.

Виды индекса доходности, в зависимости от специфики учета затрат:

1. PI с учетом дисконтированных затрат – соотношение суммы объемов дисконтированных поступлений капитала к его дисконтированному оттоку.
2. Индекс доходности – отношение всего объема произведенных инвестиций к общему оттоку средств.

Таким образом, расчет может включать либо дисконтированные, либо не дисконтированные денежные потоки

Важно – сумма инвестиций должна учитываться полностью, за все годы исполнения проекта, также в их составе должны быть учтены затраты на покрытие выбывающих фондов, понесенные до старта проекта

Что демонстрирует показатель прибыльности

Данный показатель демонстрирует эффективность использования средств в бизнес-плане либо инвестиционном проекте. Характерно, что оценка будет одинаковой как для дисконтированного, так и обычного индексов рентабельности. В приведенной ниже таблице оценивается проект с точки зрения индекса дисконтированной прибыльности (DРІ).

Таблица №1. Анализ инвестиционного проекта

Полученное значение	Анализ инвестиционного проекта
DРІ равно 1	Объем инвестиционных доходов будет таким же, как объем капиталовложений.
DРІ меньше 1	Проект убыточен, поэтому должен быть исключен из рассмотрения.
DРІ больше 1	Проект на 100% должен быть принят для дальнейших инвестиционных исследований.
DРІ-1 больше DРІ-2	В первом проекте показатель эффективности управления средствами выше, чем во втором. Привлекательность первого проекта с точки зрения капиталовложений выше.

Как определить индекс рентабельности проекта с помощью программы ExcelРассмотрим пример оценки индекса при помощи известной утилиты Excel. В данном случае придется рассчитать сразу два элемента индекса:

• чистые расходы, если те присутствовали в процессе реализации;
• чистую прибыль.

Вариант 1

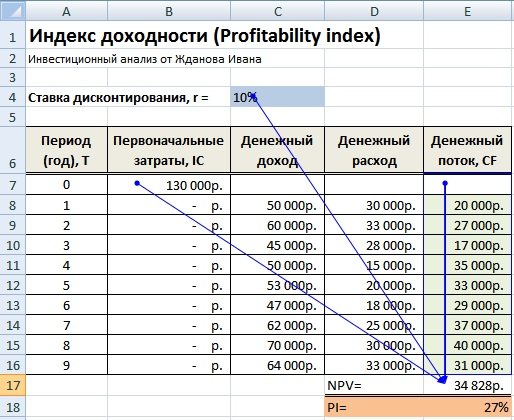
1. Показатель прибыльности – F17/В7.
2. Чистый финансовый поток – СУММ(F8/F16)-В7.
3. Дисконтированный финансовый поток – Е8(1+$М$4)˄А8.
4. Финансовый поток СF – С8-D8.

Результаты расчетов индекса приведены на изображении ниже.

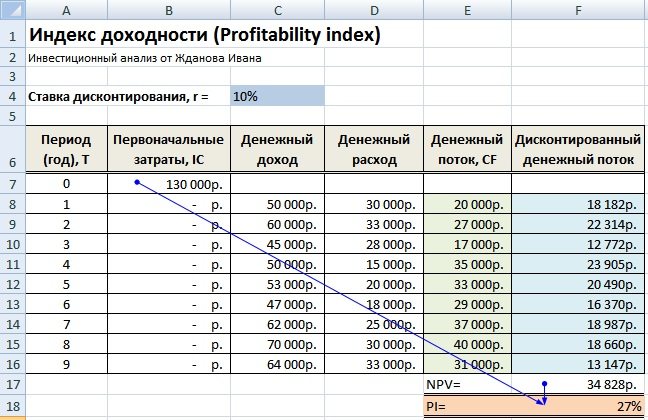
Результаты расчетов индекса

Вариант 2

Заключается в применении встроенной в программу формулы, которая называется ЧПС и используется как раз для определения необходимого нам показателя. Сама формула в данном случае будет выглядеть примерно следующим образом.

1. Показатель рентабельности – Е17/В7.
2. Дисконтированный финансовый поток – ЧПС(С4;Е7:Е16)-В7.

Как видно по второму примеру расчетов, исследования показали аналогичный результат.

Индекс доходности

Индекс доходности инвестиций

Индекс доходности инвестиций, также как и , дает инвестору наглядное представление о целесообразности вложений при выборе проектов. Этот показатель показывает уровень отдачи на вложенный рубль инвестиций. Он определяется как отношение суммы дисконтированных доходов к первоначальным инвестициям в проект, т.е.:

• CFt – денежный поток от инвестиций в t-м году;
• Io – начальные инвестиции в проект;
• n – период жизни инвестиционного проекта;
• r – процент дисконта.

Если сумма доходов меньше размера инвестиций, то проект не окупает себя и не может рассматриваться к применению. Если PI>1 проект может быть принят.

Более точным показателем является индекс доходности дисконтированных инвестиций (DPI), который определяется как:

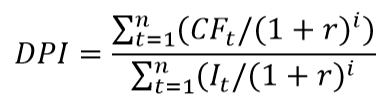
где:

It – размер инвестиций в t-ом году.

Данный показатель рассчитывается главным образом при разнесенных по времени инвестициях в один и тот же инвестиционный проект.

Например:

Срок жизни проекта 5 лет.

• Инвестиции в размере 12 млн. рублей вносятся: в 1 год жизни проекта 7млн. рублей, 2-й год 3млн. рублей и в 3-й год 2 млн. рублей.
• Доходы по годам составят: 1год – 2млн.руб.; 2 год – 3 млн. руб.; 3 год -2 млн. руб.; 4 год – 3 млн руб.; 5 год – 1 млн. руб.
• Норма дисконта 12%.

Тогда:

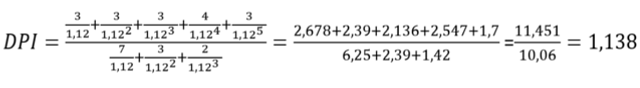
Дисконтированный индекс доходности инвестиционного проекта DPI >1, поэтому проект может быть принят к исполнению. Если бы расчет проводился при инвестиционных вложениях произведенных единовременно в начале проекта, то:

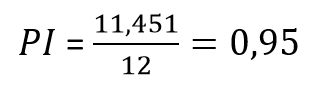
Сравнивая этот показатель с доходностью капитала инвестируемого объекта можно оценивать его целесообразность.

Расчет показателя осуществляется путем последовательных итераций до момента, когда чистая приведенная стоимость NPV меняет знак «минус» на знак «плюс». Для этого расчета используются таблицы дисконтируемых множителей, с помощью которых находят ту норму доходности, при которой NPV=0.

Более наглядным расчет выглядит в графическом изображении:

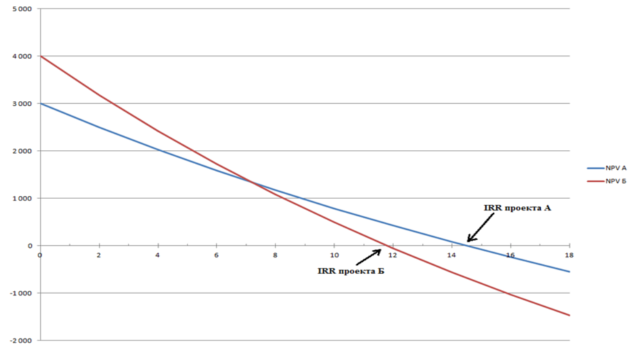
На графике представлены изменения NPV двух инвестиционных проектов: А и Б. Их NPV отражаются по оси ординат, а норма доходности отражается % по оси абсцисс. Пересечение NPV проектов с осью абсцисс дает показания их внутренней нормы доходности: для проекта А она равна 14,7%, а для проекта Б 11,8%. При доходности капитала инвестируемого объекта в 12% проект Б не может быть принят к исполнению, да и проект А не обладает необходимым запасом устойчивости по показателю доходности. Также следует оценивать проекты при кредитной ставке привлекаемых ресурсов в 11% годовых.

Сразу надо отметить, что если денежные потоки на протяжении исследуемого периода времени меняют знак с плюса на минус или наоборот, то расчет IRR становится невозможным, а если его рассчитывают, то он не отражает реальной нормы доходности проекта.

Для нашего вышеприведенного примера, когда PI показывает негативные результаты, рассчитаем IRR с применением таблиц дисконтируемых множителей. Выберем норму доходности близкую к расчетной r=11% и r=12%.

Год Денежный поток млн.руб. Расчет 1 Расчет 2 r= 11% NPV r= 12% NPV 1 -12+3 1,0 -9,0 1,0 -9,0 2 3 1,110 -6,297 1,12 -6,322 3 3 1,232 -3,861 1,254 -4,186 4 4 1,368 -0,937 1,405 -1,639 5 3 1,518 0,999 1,574 0,061 Итого 4 0,999 0,061

При r=12% NPV практически равно 0, то есть внутренняя норма доходности равна ~12% и все проекты с доходностью менее этой величины не могут приниматься в работу. В нашем случае норма дисконта равна внутренней норме доходности, но проект с единовременными вложениями в 12 млн. рублей отклоняется, поскольку PI= 0,95.

Все эти показатели при расчете целесообразности инвестирования одного проекта не противоречат друг другу. Так в нашем примере:

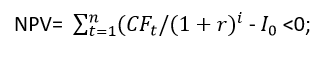
PI <1;

IRR ≤ r.

Поэтому инвестиционный проект не представляет интереса для инвестора.

Обычно инвесторы принимают к рассмотрению проекты, превосходящие внутреннюю норму доходности на 7-8% больше чем норма дисконта, которую принимают равной доходности капитала инвестируемого объекта или кредитной ставки на банковские ресурсы.

Читайте так же про критерии оценки инвестиционного проекта.