Округление

Как округлить до трех значащих цифр в Excel

В Excel все решает пользователь. Программа округлит дробные или даже целые числа в зависимости какое число значащих цифр удовлетворит потребность пользователя. Несомненно, на первый взгляд такое округление может вызывать сомнение в рациональности решения. Однако в презентациях есть место быть как точным показателям, так и относительным. И в других ситуациях это также применимо. Например, в стратегическом планировании более важные относительные показатели, так как сколько не планируй никогда не угадаешь точные результирующие числа. В тактическом планировании более важны точные значения чтобы избежать серьезных просчетов. В стратегическом планировании где показатели достигают миллионов, каждое значение ниже определенного числа значащих цифр – не существенно.

Ниже на рисунке показано, как составить формулу, которая округляет миллионные числовые значения до заданного числа значащих цифр:

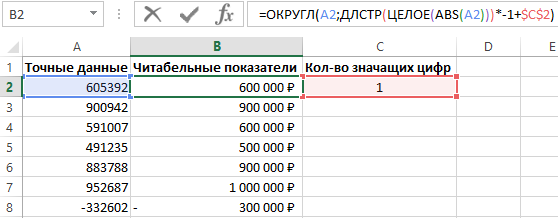
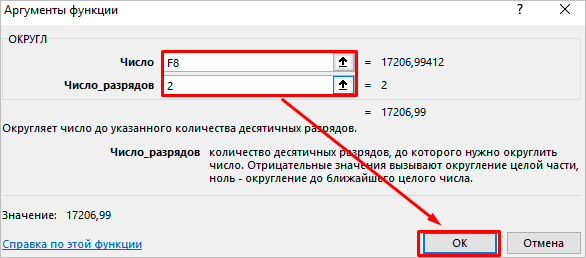
Функция ОКРУГЛ используется для округления исходного числового значения до определенного количества разрядов после запятой. Функция содержит 2 аргумента:

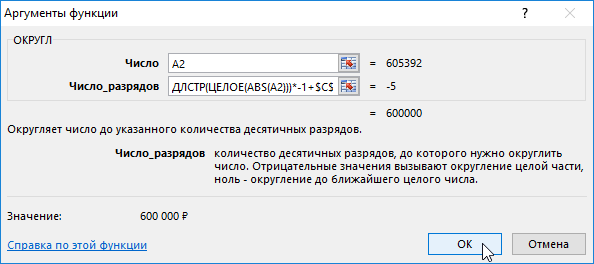
1. Число – ссылка на исходное значение, которое необходимо округлить.
2. Число-разрядов – количество разрядов, которое необходимо оставить после округления исходного числа.

Если во втором аргументе функции ОКРУГЛ указать отрицательное число, тогда Excel округлит исходное числовое значение в соответствии цифр по левой стороне запятой. Например, следующая формула возвращает в результате вычисления число 9500:

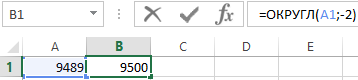
А если указать во втором аргументе значение -3, тогда функция ОКРУГЛ возвращает результат 9000:

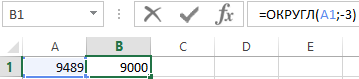
Такая формула прекрасно работает, но не всегда. Например, что будет если исходные числовые значения будут разных величин числовых радов? Одни будут более миллиона, другие едва превышают сотни тысяч. Если возникнет необходимость округлить все такие исходные значения до одной и той же значащей цифры используя при этом одну и туже формулу (как обычно принято в Excel). Применять для отдельных групп исходных значений функцию ОКГРУГЛ с разными значениями в аргументах – это не правильное, а точнее не наилучшее решение. Хотя теоретически все может сработать.

Для красивого решения данной задачи следует использовать постоянное неизменяемое число значащих цифр в формуле, которая вычислит соответствующие значения.

Округление при работе с числами ограниченной точности

Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах погрешности измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.

Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,40 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.

Округление рассчитанного значения погрешности

Обычно в окончательном значении рассчитанной погрешности оставляют только первые одну-две значащие цифры. По одному из применяемых правил, если значение погрешности начинается с цифр 1 или 2(по другому правилу — 1, 2 или 3), то в нём сохраняют две значащих цифры, в остальных случаях — одну, например: 0,13; 0,26; 0,3; 0,8. То есть каждая декада возможных значений округляемой погрешности разделена на две части. Недостаток этого правила состоит в том, что относительная погрешность округления изменяется значительным скачком при переходе от числа 0,29 к числу 0,3. Для устранения этого предлагается каждую декаду возможных значений погрешности делить на три части с менее резким изменением шага округления. Тогда ряд разрешённых к употреблению округлённых значений погрешности получает вид:

• 0,10; 0,12; 0,14; 0,16; 0,18;
• 0,20; 0,25; 0,30; 0,35; 0,40; 0,45;
• 0,5; 0,6; 0,7; 0,8; 0,9; 1,0.

Однако при использовании такого правила последние цифры самого результата, оставляемые после округления, также должны соответствовать приведённому ряду.

Пересчёт значений физических величин

Пересчёт значения физической величины из одной системы единиц в другую должен производиться с сохранением точности исходного значения. Для этого исходное значение в одних единицах следует умножить (разделить) на переводной коэффициент, часто содержащий большое количество значащих цифр, и округлить полученный результат до количества значащих цифр, обеспечивающего точность исходного значения. Например, при пересчёте значения силы 96,3 тс в значение, выраженное в килоньютонах (кН), следует умножить исходное значение на переводной коэффициент 9,80665 (1 тс = 9,80665 кН). В результате получается значение 944,380395 кН, которое необходимо округлить до трёх значащих цифр. Вместо 96,3 тс получаем 944 кН.

Примечания

1. ↑
2.  (недоступная ссылка). Дата обращения: 8 августа 2015.
3. Кнут Д. Э. Искусство программирования. Том 1. Основные алгоритмы = The Art of Computer Programming. Volume 1. Fundamental Algorithms / под ред. С. Г. Тригуб (гл. 1), Ю. Г. Гордиенко (гл. 2) и И. В. Красикова (разд. 2.5 и 2.6). — 3. — Москва: Вильямс, 2002. — Т. 1. — 720 с. — ISBN 5-8459-0080-8.
4. A’Hearn, B., J. Baten, D. Crayen (2009). «Quantifying Quantitative Literacy: Age Heaping and the History of Human Capital», Journal of Economic History 69, 783—808.
5. ↑ . www.metrologie.ru. Дата обращения: 10 августа 2019.
6. . StudFiles. Дата обращения: 10 августа 2019.
7. . sv777.ru. Дата обращения: 8 августа 2019.
8. В. М. Заварыкин, В. Г. Житомирский, М. П. Лапчик. Техника вычислений и алгоритмизация: Вводный курс: Учебное пособие для студентов педагогических институтов по физико-математическим специальностям. — М: Просвещение, 1987. 160 с.: ил.
9. цит. по В. Гильде, З. Альтрихтер. «С микрокалькулятором в руках». Издание второе. Перевод с немецкого Ю. А. Данилова. М:Мир, 1987, стр. 64.

Приближённые значения

Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-то найти невозможно, или же не важно чтобы это значение было точным для исследуемого предмета. Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают

Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек

Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.

Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».

В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:

Читается как «приближённо (приблизительно) равно».

Чтобы указать приближённое (приблизительное) значение, прибегают к такому действию как округление чисел.

ДРУГОЕ

Как округлить число в excel?

Программа Microsoft Excel – одно из приложений пакета Microsoft Office, предназначенное, в том числе, для произведения…

Правила округления

В некоторых случаях, точное число при делении определенной суммы на конкретное число невозможно определить в принципе.…

Правила деления на числа от 1 до 10, а также на 11 и 25 были выведены, чтобы упростить процесс деления натуральных…

Часто при расчетах в результате получается не целое число, а десятичная дробь — число с несколькими знаками после…

Когда при расчетах не нужна супер точность, возникает необходимость округления десятичных дробей до десятых. В…

Как округлять числа?

Округление чисел — простейшая математическая операция. Чтобы уметь правильно округлять числа, необходимо знать три…

Как посчитать процент от числа?

Для того чтобы узнать, как посчитать процент от числа, нужно сначала разобраться, что такое процент.Процент — это одна…

Как возводить в дробную степень?

Иногда в математике необходимо возвести число в степень, которая представляет собой дробь. О том, как возвести число в…

Сколько существует цифр?

Математика — область абстрактных знаний. Но, несмотря на это, мы автоматически не замечаем, что многое, что изучает эта…

Как перевести дробь в число?

Дробь может быть преобразована в целое число либо в десятичную дробь. Неправильная дробь, числитель которой больше…

Как перевести десятичную дробь в обыкновенную?

Десятичная дробь состоит из двух частей, которые разделены запятыми. Первая часть — это целая единица, вторая часть -…

Как складывать дроби?

Чтобы понять, как складывать дроби надо, прежде всего, знать классификацию дроби.Виды дробиОбыкновенные дробиПравильные…

Вопрос о том, как умножать дроби задает себе не только школьник. Порой и родители в порыве желания помочь своему чаду…

Для написания римских цифр стоит использовать следующие буквы латинского алфавита. Не менее древнего кстати. На…

Как записывать числа?

С древних времен люди понимали необходимость в подсчете всего, что их окружает — предметов, денег, времени и прочего.…

В математике дробь — это число, состоящее из одной или нескольких долей единицы. То есть дробь представляет собой…

Как правильно писать «так как»?

Знание своего языка и грамотность нужны любому человеку в повседневной жизни. Сегодня поговорим об интересных союзе и…

В русском языке множество слов можно писать правильно и при этом даже не задумываться о конкретных случаях…

Как выделяется запятыми «в том числе»?

В том числе — союз, употребляемый для уточнения или дополнения информации с помощью присоединения члена предложения,…

Точка с запятой — это знак препинания, который отделяет части предложения друг от друга, не является парным. Многие…

Способы записи числа

Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:

Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как или для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.

В JavaScript можно использовать букву , чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:

Другими словами, производит операцию умножения числа на 1 с указанным количеством нулей.

Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):

Записать микросекунду в укороченном виде нам поможет .

Если мы подсчитаем количество нулей , их будет 6. Естественно, верная запись .

Другими словами, отрицательное число после подразумевает деление на 1 с указанным количеством нулей:

Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: , после которого указывается число.

Например:

Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются для двоичных и для восьмеричных:

Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию (рассмотрим позже в этой главе).

Общий порядок округления и терминология

• Округление числа, записанного в позиционной системе счисления с M знаками дробной части, может производиться «до K-го знака после запятой», где K ≤ M. При таком округлении в записи числа отбрасываются справа (M-K) значащих цифр, а K-я цифра после запятой может измениться (см. ). Применяется также терминология с указанием единицы наименьшей десятичной доли, сохраняющейся у округлённого числа, то есть «округление до десятых», «…до сотых», «…до тысячных» и т. д. (соответствует округлению до одного, двух, трёх и так далее знаков после запятой). Частный случай, когда K=0, называется «округлением до целого».
• Когда при округлении отбрасываются значащие цифры целой части числа, говорят об «округлении до десятков» (сотен, тысяч и так далее), отбрасывая, соответственно, один, два, три и более знака. При таком округлении отбрасываемые цифры целой части числа заменяются на нули.
• Для чисел, представленных в нормализованном виде, говорят об «округлении до K (значащих) цифр». При этом мантисса числа сохраняет K значащих цифр, остальные цифры справа отбрасываются.

Как работать с функциями в Excel

Мы рассмотрели самый простой способ убрать лишние знаки. Использовать его довольно удобно, если менять сами данные в таблице нам не нужно. Теперь мы переходим к использованию различных функций. Но сначала я хочу напомнить вам, что это такое, а также как с ними работать.

Функции ускоряют и упрощают вычисления. Например, нам надо посчитать сумму в столбце, в котором 100 значений. Мы можем делать это самым прямым способом “1+20+30+43…” и так 99 раз. Или написать встроенную команду “СУММ”, указать диапазон ячеек, и программа за секунду сделает расчеты.

Первый способ

Чтобы вручную написать формулу в ячейке с использованием функции, обязательно нужно:

1. Поставить знак =.
2. Правильно указать название.
3. Открыть круглую скобку.
4. Указать через точку с запятой аргументы, то есть данные, которые будут использоваться.
5. Закрыть скобку.

Что может выступать аргументом математических формул:

• число,
• формула,
• диапазон ячеек.

Пример: функция “=СУММ(F21:F30)” посчитает сумму чисел, написанных в столбце F с позиции F21 до F30.

Эти правила нужно запомнить, иначе программа не сможет сделать вычисления, а будет выдавать ошибку такого вида.

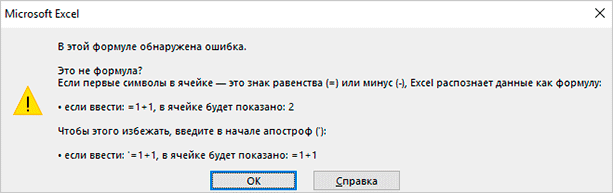
Второй способ

Если неудобно писать команды вручную, то можно воспользоваться библиотекой, которая находится во вкладке “Формулы”.

Нас в данный момент интересуют математические операции. Нажимаем на соответствующий раздел и выбираем нужную процедуру.

Откроется диалоговое окно, в котором легко понять, какие аргументы нужно указать. Заполните поля и нажмите “ОК”.

Способы округления чисел

Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.

Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .

math.ceil() — округление чисел в большую сторону

Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.

Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.

Пример:

math.ceil(5.15) # = 6
math.ceil(6.666) # = 7
math.ceil(5) # = 5

Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.

math.floor() — округление чисел в меньшую сторону

Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.

Пример:

math.floor(7.9) # = 7
math.floor(9.999) # = 9
math.floor(-6.1) # = -7

math.trunc() — отбрасывание дробной части

Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.

Примеры:

math.trunc(5.51) # = 5
math.trunc(-6.99) # = -6

Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .

Примеры:

int(5.51) # = 5
int(-6.99) # = -6

Нормальное округление

Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.

И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().

Примеры:

math.floor(9.999) # = 9
int(9.999) # = 9
math.ceil(-9.999) # = -9
int(-9.999) # = -9

Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.

Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:

def int_r(num):
    num = int(num + (0.5 if num > 0 else -0.5))
    return num

Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).

Примеры:

int_r(11.5) # = 12
int_r(11.4) # = 11
int_r(-0.991) # = -1
int_r(1.391) # = 1

round() — округление чисел

round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.

В Python 2

Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.

Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».

Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.

В Python 3

В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.

Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.

Примеры:

round(3.5) # = 4
round(9.5) # = 10
round(6.5) # = 6
round(-6.5) # = -6
round(-7.5) # = -8

Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.

Округление до сотых

У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.

Пример округления до нужного знака:

round(3.555, 2) # = 3.56
round(9.515,1) # = 9.5
round(6.657,2) # = 6.66

Правила округления

Коммерческое округление

В Коммерческие туры (не отрицательные числа) выглядит следующим образом :

• Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
• Если число в первом десятичном разряде — 5, 6, 7, 8 или 9, то оно округляется в большую сторону.

Это правило округления описано в стандарте DIN 1333 . Округление часто уже преподается в начальной школе.

Примеры (округление до двух знаков после запятой):

• 13,3749 … € ≈ 13,37 €
• 13,3750 … € ≈ 13,38 €

Отрицательные числа в зависимости от их величины округлой формы, на 5 , чтобы сказать от нуля ( Engl : от нуля ):

• −13,3749 … € ≈ −13,37 €
• −13,3750 … € ≈ −13,38 €

В Коммерческих турах частично в правовой среде , как гражданские раунды , называемых и г. Б. в о поставщиках государственных услуг пояснил следующее:

Симметричное закругление

Коммерческое и симметричное округление отличаются друг от друга только тем, что число округляется точно посередине между двумя числами с выбранным количеством десятичных цифр.

Симметричные (или геодезическим, математический, искажаются, научный ) округление определяются следующим образом (композиция адаптирована):

1. Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
2. Если число представляет собой 5 (за которыми следуют другие цифры, которые не равны нулю), 6, 7, 8 или 9 в первом десятичном разряде, оно округляется в большую сторону.
3. Если цифра в первом десятичном разряде, которую следует опустить, представляет собой только 5 (или 5, за которой следуют только нули), она округляется таким образом, чтобы последняя сохраняемая цифра была четной.

Этот тип округления используется в числовой математике , инженерии и технике. Он предусмотрен стандартом IEEE 754 для вычислений с двоичными числами с плавающей запятой в компьютерах. В англоязычной литературе это называется Round to Even или Banker’s Rounding .

Примеры (округление до одного десятичного знака):

• 2,2499 ≈ 2,2 (по правилу 1)
• 2,2501 ≈ 2,3 (по правилу 2)
• 2,2500 ≈ 2,2 (округлено до четного числа согласно правилу 3)
• 2,3500 ≈ 2,4 (округлено до четного числа согласно правилу 3)

Коммерческое округление приводит к небольшим систематическим ошибкам, так как округление на 0,5 происходит в большую сторону, а в меньшую сторону на 0,5 никогда не происходит; это может немного исказить статистику. Математическое округление всегда округляется в большую или меньшую сторону от точной середины между двумя цифрами до следующей четной цифры. В результате среднее значение округляется вверх и вниз примерно так же часто, по крайней мере, если исходные числа являются стохастическими . (Контрпример: если маленькие числа встречаются чаще, чем большие, их можно систематически округлять в меньшую сторону, чем в большую, см . Закон Бенфорда .)

Округление с сохранением суммы

В случае округления с сохранением суммы слагаемые округляются так, чтобы их сумма была равна округленной сумме слагаемых. Может потребоваться округлить некоторые слагаемые от ближайшего округленного значения до противоположного значения.

Важными приложениями являются распределение мест в пропорциональном представительстве и распределение всего НДС в счете-фактуре по его отдельным позициям.

Случай, когда все слагаемые положительные, был тщательно исследован, см. Процедуру распределения мест .

Метод Харе-Нимейера может быть обобщен для слагаемых с обоими знаками : вы округляете все числа до ближайших круглых чисел, и пока сумма слишком велика (или слишком мала), вы выбираете одно из округленных (или округленных) чисел. ) нумерует с наибольшим округление (или самое большое количество округления вниз) и изменяет его округления в направлении , противоположном. Это означает, что сумма изменений минимальна .

toString(base)

Метод возвращает строковое представление числа в системе счисления .

Например:

может варьироваться от до (по умолчанию ).

Часто используемые:

• base=16 — для шестнадцатеричного представления цвета, кодировки символов и т.д., цифры могут быть или .

• base=2 — обычно используется для отладки побитовых операций, цифры или .

• base=36 — максимальное основание, цифры могут быть или . То есть, используется весь латинский алфавит для представления числа. Забавно, но можно использовать -разрядную систему счисления для получения короткого представления большого числового идентификатора. К примеру, для создания короткой ссылки. Для этого просто преобразуем его в -разрядную систему счисления:

Две точки для вызова метода

Внимание! Две точки в это не опечатка. Если нам надо вызвать метод непосредственно на числе, как в примере выше, то нам надо поставить две точки после числа

Если мы поставим одну точку: , тогда это будет ошибкой, поскольку синтаксис JavaScript предполагает, что после первой точки начинается десятичная часть. А если поставить две точки, то JavaScript понимает, что десятичная часть отсутствует, и начинается метод.

Также можно записать как .

Как округлять числа в Google Таблицах (используя функцию ОКРУГЛЕНИЯ)

Синтаксис функции ROUND (ОКРУГЛ) следующий:

ROUND(value, )

Здесь,

• value — это число, которое нужно округлить. Это может быть числовое значение или ссылка на ячейку, содержащую числовое значение.
• Places — это количество цифр или десятичных знаков, до которых вы хотите округлить значение. Этот параметр не является обязательным. Если он не указан, по умолчанию предполагается, что его значение равно 0.

Давайте рассмотрим несколько примеров и попытаемся округлить заданные значения столбца A до количества мест, указанного в столбце B, с помощью функции ROUND:

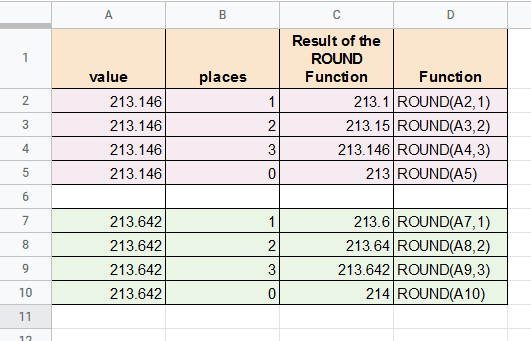
На изображении выше вы увидите, что:

• В строке 2 мы хотим округлить значение 213,146 до 1 десятичного знака. Согласно стандартным правилам округления цифра округления 1 остается прежней. Итак, округленное число теперь становится 213,1 . Мы фактически «округлили» значение 213,145 в меньшую сторону .
• В строке 3 мы хотим округлить значение 213,146 до 2 знаков после запятой. Согласно стандартным правилам округления цифра округления 4 увеличивается на 1. Округленное число теперь становится 213,15 . По сути, мы округлили значение 213,145 .
• В строке 5 в формуле отсутствует параметр мест, поэтому будет использоваться значение по умолчанию 0. Это означает, что мы хотим округлить значение 213,146 до 0 десятичных знаков, другими словами, до ближайшего целого числа. Согласно стандартным правилам округления, ближайшее целое число к 213,146 равно 213 . И снова мы округлили значение 213,146 в меньшую сторону .
• В строке 10 снова отсутствует параметр мест. Итак, нам снова нужно округлить значение до ближайшего целого числа. Ближайшее целое число к 213,642 — 214 . Здесь мы, по сути, «округлили» значение 213,642 .

Функцию ОКРУГЛ также можно использовать с отрицательными значениями параметра places. В таких случаях значение округляется слева от десятичной точки. Так,

• если разряды равно -1, функция ОКРУГЛ округляет значение до ближайших десятков.
• если количество мест равно -2, функция ОКРУГЛ округляет значение до ближайших сотен.
• если разряды равно -3, функция ОКРУГЛ округляет значение до ближайших тысяч.

и так далее.

Давайте рассмотрим еще несколько примеров, чтобы понять, как функция ROUND работает с отрицательными значениями параметра place:

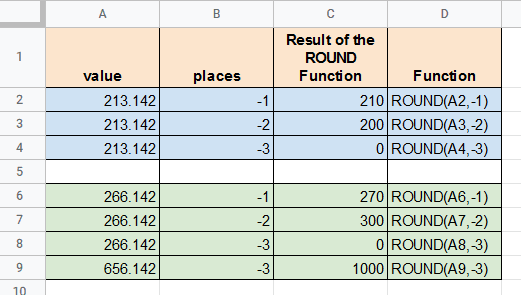
На изображении выше вы увидите, что:

• В строке 2 мы округляем значение 213,146 до -1 разряда . Функция удаляет все цифры справа от десятичной точки. Затем он округляет значение слева от десятичной точки до ближайших десятков. Ближайшая к числу 13 десятка — 10 . Итак, функция округляет значение до 210 .
• В строке 3 округляем значение 213,146 до -2 разряда . Функция округляет целую часть значения до ближайших сотен. Ближайшая сотня к числу 213 — 200 . Итак, функция округляет значение до 200 .
• В строке 6 округляем значение 266,142 до -1 разряда . Функция округляет целую часть значения до ближайших десятков. Ближайшая к числу 66 десятка равна 70. Итак, функция округляет значение до 270 .
• В строке 9 округляем значение 656,142 до -3 разряда . Функция округляет целую часть значения до ближайших тысяч. Ближайшие тысячи к числу 656 — 1000 . Итак, функция округляет значение до 1000 .

Из приведенных выше примеров ясно, что функция ROUND либо округляет заданное значение в большую, либо в меньшую сторону, в зависимости от стандартных правил округления. Но что, если вы хотите, чтобы ваша ценность округлялась только в большую сторону, а не в меньшую?

В таких случаях вы можете использовать функцию ROUNDUP Google Таблицах.