Дюрация облигации

???? Основные типы

Финансовый рынок предлагает огромное множество облигаций. Начинающему инвестору легко запутаться в этом многообразии. Кратко рассмотрим основные виды облигаций.

По типу эмитента

Виды:

1. Государственные – считаются одними из наиболее надежных среди ценных бумаг. В России самые распространенные бумаги данной категории – это облигации федерального займа (ОФЗ). Они характеризуются хорошей ликвидностью, минимальной вероятностью дефолта эмитента, но доходность их относительно невысока из-за низких кредитных рисков.
2. Корпоративные – выпускаются юридическими лицами – отдельными компаниями. Их доходность обычно выше, чем у ОФЗ. Среди корпоративных бумаг особняком стоят субординированные облигации. Это заем компании, ранг которого ниже, чем у остальных долговых обязательств. Инвесторы субординированных облигаций получают свою долю при банкротстве компании в самую последнюю очередь, исключение составляют акционеры компании, держащие субординированные бумаги. Субординированные облигации имеют повышенную доходность, но и дополнительный риск для вкладчиков. Нужно учитывать это при формировании своего инвестиционного портфеля.
3. Муниципальные – выпускаются муниципальными образованиями, и их рынок довольно мал. Уровень кредитного риска у таких бумаг выше, чем у государственных, поскольку – разумеется – государство будет всеми возможными способами помогать региону выполнять свои обязательства, но дефолт эмитента все же допускается. Поэтому приравнивать муниципальные облигации по надежности к государственным (например, к ОФЗ) некорректно.
4. Иностранные (международные) – выпускаются иностранными эмитентами, государственными или частными. При этом номинированы не в той валюте, в которой расположен эмитент. Часто размещаются инвестиционными банками, а покупателями являются страховые, инвестиционные компании и т. д.

Вы инвестируете в облигации?

Да, выбираю старые добрые ОФЗДа, предпочитаю рисковать, но покупать доходные бумагиЯ даже не знаю, что такое облигация

По типу дохода

Виды:

1. С фиксированным купоном – это облигации с определенной процентной ставкой, которая выплачивается через установленные промежутки времени.
2. С переменным купоном – часто встречаются среди корпоративных бумаг. Доход меняется в зависимости от изменения рыночных ставок. На практике это выглядит так: купон фиксируется до даты оферты, после чего процентная ставка меняется в зависимости от конъюнктуры. До оферты новая процентная ставка неизвестна. Такие облигации выгодны эмитенту, поскольку позволяют уменьшить процентные риски в случаях, когда выпуск облигаций приходится на период высоких процентов, после которых на рынке ожидается понижение. У таких облигаций доходность принято считать не к сроку погашения, а к сроку ближайшей оферты. Офертой по облигациям называется предложение о досрочном погашении облигации эмитентом по заранее оговоренной стоимости.
3. С индексируемым купоном – это облигации, доходность которых напрямую зависит от инфляции (или иного финансового инструмента). В этом случае номинал облигации индексируется на величину инфляции. Размер купона обычно рассчитывается на один купонный период, поскольку номинал облигации, от размера которого и зависит купон, меняется в соответствии с показателем инфляции. Иногда процентная ставка может быть привязана к другому финансовому инструменту – курс доллара, ставке RUONIA и т. д.

По типу погашения

Виды:

1. С погашением полностью в конце срока – номинал единым платежом выплачивается инвестору в полном размере в дату погашения облигации.
2. С амортизируемым долгом – когда номинал частично погашается до срока погашения облигации. Это происходит, если эмитенту неудобно выплачивать сразу большую сумму в срок погашения. Тогда номинал погашается частями параллельно с выплатами по купону, и в результате эмитент выплачивает долг равными частями во время всего периода обращения облигации.

По сроку размещения

Деление довольно условно, поскольку в разных странах показатели могут меняться. Если брать усредненные значения, то облигации бывают:

• краткосрочные – срок погашения до 2 лет;
• среднесрочные – срок погашения от 3 до 7 лет;
• долгосрочные – срок погашения более 7 лет.

Деноминация. Положительные и отрицательные последствия проведения
Читать

Девальвация. Понятие, причины, влияние на население и государство
Подробнее

Что такое инфляция. Виды, причины, методы измерения
Смотреть

Дюрация некоторых потоков платежей[править | править код]

Дюрация аннуитета

Можно показать, что дюрация аннуитета, ограниченного сроком T

, равна следующей величине: D = 1 + r r − T ( 1 + r ) T − 1 . {\displaystyle D={\frac {1+r}{r}}-{\frac {T}{(1+r)^{T}-1}}.} Модифицированную дюрацию можно получить разделением на 1 + r {\displaystyle 1+r} .

Здесь в формуле подразумевается эффективная ставка за интервал аннуитета и срок и дюрацию также в интервалах аннуитета. Если использовать годовую эффективную ставку, то для дюрации в годах формула будет такой

D = t × ( 1 + r ) t ( 1 + r ) t − 1 − T ( 1 + r ) T − 1 , {\displaystyle D=t\times {\frac {(1+r)^{t}}{(1+r)^{t}-1}}-{\frac {T}{(1+r)^{T}-1}},}

где t {\displaystyle t} — длительность интервала аннуитета в годах (доля года), T {\displaystyle T} — срок аннуитета в годах, r {\displaystyle r} — годовая эффективная ставка. При t

= 1 получаем прежнюю формулу.

Для вечного аннуитета формулу дюрации можно определить как предел приведенной формулы при T → ∞ {\displaystyle T\rightarrow \infty } (второе слагаемое в этом случае будет стремиться к нулю). Можно также вывести формулу непосредственно. Приведенная стоимость вечного аннуитета равна P V = A / r {\displaystyle PV=A/r} . Воспользуемся формулой через производную. Производная этой функции по r {\displaystyle r} , очевидно равна − A / r 2 {\displaystyle -A/r^{2}} . Умножая эту величину на ( 1 + r ) {\displaystyle (1+r)} и разделив на P V {\displaystyle PV} , получим окончательно формулу дюрации:

D = ( 1 + r ) / r . {\displaystyle D=(1+r)/r.}

Модифицированная дюрация, очевидно равна в этом случае M D = 1 / r {\displaystyle MD=1/r} .

Дюрация облигации

Для бескупонной облигации номиналом N {\displaystyle N} со сроком погашения t {\displaystyle t} текущая стоимость равна

P V = N / ( 1 + r ) t . {\displaystyle PV=N/(1+r)^{t}.}

Она же совпадает с дисконтированной стоимостью единственного платежа, поэтому её дюрация просто равна сроку облигации:

D = t . {\displaystyle D=t.}

В случае купонной облигации денежный поток состоит из купонных платежей и погашения номинала. При этом погашение номинала может быть частями (амортизация) и купонная ставка может, вообще говоря, изменяться в течение срока обращения облигации. Если величину купонов обозначить C i {\displaystyle C_{i}} , а погашения номинала N j {\displaystyle N_{j}} , то дюрация облигации будет равна

D = ∑ i = 1 m C i ( 1 + r ) t i t i + ∑ j = 1 k N j ( 1 + r ) t j t j P , {\displaystyle D={\frac {\sum _{i=1}^{m}{\frac {C_{i}}{(1+r)^{t_{i}}}}t_{i}+\sum _{j=1}^{k}{\frac {N_{j}}{(1+r)^{t_{j}}}}t_{j}}{P}},}

где P {\displaystyle P} — цена облигации (предполагается что в качестве r {\displaystyle r} используется доходность к погашению облигации, поэтому P V ( r ) = P {\displaystyle PV(r)=P} ).

Формула будет иметь точно такой же вид, если вместо величины купонов C i {\displaystyle C_{i}} использовать соответствующие купонные ставки, вместо сумм погашений номинала N j {\displaystyle N_{j}} — доли погашений номинала, а вместо цены облигации в денежном выражении P {\displaystyle P} использовать стандартную цену в процентах (долях) от номинала.

При прочих равных условиях, чем больше срок погашения и (или) ниже купонная ставка и (или) ниже доходность к погашению, тем больше дюрация облигации. При прочих равных условиях чем чаще выплачивается купон, тем меньше дюрация.

В простейшем случае постоянной купонной ставки и единовременного погашения номинала в конце срока для расчета дюрации можно использовать встроенную в Microsoft Office Excel 2007 функцию ДЛИТ

Примеры для чего нужна и где используется

Дюрация позволяет оценить рискованность вложений. Основная цель инвестора — это свести к минимуму риски потерь, при сохранении необходимого уровня доходности.

Учитывая, что на долговом рынке обращаются множество бумаг с различным периодом обращения, доходностью и разными выплатами по купонам, нужен некий параметр, способный провести их сравнение.

Одним из них выступает дюрация.

Для лучшего понимания разберем на примерах их реальной жизни.

Пример 1.

У вас просят занять 100 тысяч рублей под 10% годовых сроком на год 2 человека: Иван Петрович и дядя Вася.

Иван Петрович предлагает выплачивать вам проценты за пользование каждый месяц. И возврат всей суммы долга в конце срока.

Дядя Вася не может платить ежемесячно. Но обещает вернуть всю сумму целиком с процентами через год.

Кому бы вы заняли денег?

Ответ очевиден. Конечно же Ивану Петровичу.

А почему? Вы сразу же начинаете получать прибыль уже в первый месяц. И риск того, что долг не будет возвращен полностью или частично тоже ниже.

Аналогично работает и дюрация. При одинаковой доходности 2-х бумаг (с одинаковым кредитным рейтингом), выбираем облигацию с наименьшей дюрацией.

Пример 2.

Иван Петрович и дядя Вася опять хотят денег. Снова 100 тысяч под 10% годовых.  Только Иван Петрович просит дать ему в долг на 3 года. А дядя Вася на 10 лет. Оба обязуются выплачивать проценты каждый квартал.

Опять вопрос. Кого из них кредитовать?

Одолжив Ивану Петровичу, вы вернете свои деньги быстрее. Значит риски меньше. За 3-х летний срок вероятность возникновения различных ситуаций, влияющих на ценность денег гораздо ниже.

Кредитуя дядю Васю на такой длительный срок вы рискуете сильнее. Неизвестно, что может случиться за это десятилетие.

Вдруг в стране через 5 лет начнется сильнейшая инфляция и все ваши заемные средства сразу же обесценятся. Или произойдет повышение процентной ставки в стране. Когда ниже 20-30% годовых никто не будет давать в долг. И ваша доходность от дяди Васи для этого периода времени будет просто смешная. Дядя Вася может заболеть, потерять работу или просто не захотеть выплачивать вам долг.

Одолжив деньги на 3 года мы несем гораздо меньшие риски потери в будущем.

И опять все это дело показывает дюрация. По дяде Васе она будет значительно больше.

Примеры применения на практике

Теперь пришло время поговорить о том, для чего же всё-таки нужно знать такой параметр как ДО, и как его можно применять на практике.

Снижение риска инвестиций

Во-первых, как уже упоминалось выше, дюрация может служить мерой рискованности ваших инвестиций. Чем меньше величина дюрации (читай – срок окупаемости), тем меньше и риск потерять вложенные средства (или часть из них).

Для иллюстрации этого момента давайте рассмотрим простой пример. Представьте себе, что к вам пришли два человека, каждый с просьбой одолжить ему сумму в 1000000 рублей на срок в один год. Каждый из них готов уплачивать проценты в размере 15% годовых, но первый заёмщик готов платить проценты ежемесячно (а размере 15%/12 месяцев = 1,25%), а второй только по истечении года. Кому из них, при прочих равных условиях, вы предпочтёте одолжить деньги?

Ответ очевиден, наиболее выгодным для вас вариантом является одолжить деньги первому заёмщику, который согласен платить проценты ежемесячно. Этот вариант обладает тем неоспоримым преимуществом, что вы начинаете получать возврат инвестированных средств с первого же месяца. А это в свою очередь снижает риск инвестиций (ведь при одинаково неблагоприятном стечении обстоятельств, с первого заёмщика вы получите хоть что-то, в то время как со второго рискуете не получить вообще ничего).

Теперь перейдём к облигациям. Предположим, вы выбираете между двумя облигациями с одинаковыми сроками погашения и стоимостью. Но первая из этих облигаций предполагает выплату купонного дохода раз в месяц, а вторая только раз в год. Соответственно, ДО для первой облигации будет меньше, чем для второй (мы ведь помним, что ДО тем меньше, чем чаще выплачивается купонный доход по ней). И, следовательно, риск инвестиций в первые облигации будет меньшим, чем риск инвестиций во вторые облигации.

Зависимость ДО от процентной ставки

Облигации в целом являются довольно консервативным финансовым инструментом, то есть риск по ним и так минимален (он практически сопоставим с рисками по банковским депозитам). Поэтому дюрацию облигаций чаще рассматривают не в контексте снижения риска, а в контексте зависимости от процентных ставок.

Чтобы проиллюстрировать эту зависимость, давайте рассмотрим простой пример. Предположим, что вы приобрели, на одинаковые суммы денег, два вида облигаций одного и того же эмитента, но с разными сроками погашения. У первых срок погашения через год (ДО меньше), у вторых срок погашения через 10 лет (следовательно, ДО гораздо больше). Купонный доход по обоим видам облигаций составляет 10% годовых.

Теперь предположим, что процентные ставки в стране начали сильно расти и если сегодня выпускали облигации доходностью в 10%, то через некоторое время появляются новые облигации дающие доходность в 12%, а затем и в 15% и в 20%. Как вы думаете, при этом изменится стоимость ваших облигаций дающих 10% годового дохода? Правильно, их стоимость упадет, поскольку спрос на них значительно снизится (зачем людям покупать ваши «десятипроцентные» облигации по прежней цене, если они могут вложить деньги в более доходные бумаги).

Причём стоимость облигаций с большим значением ДО (у которых срок погашения через 10 лет) снизится гораздо больше, чем стоимость облигаций с меньшим значением дюрации (у которых срок погашения через год).

Представим теперь, что события стали развиваться диаметрально противоположным образом и процентные ставки в стране начали падать. То есть если сегодня вложить деньги под 10% годовых можно было относительно легко, то через некоторое время процентная ставка снизится до 5% и вложить деньги под те же 10% (с сохранением того же уровня риска) уже будет попросту невозможно. Очевидно, что при этом варианте развития событий, ваши облигации значительно вырастут в цене, ведь каждый предпочтёт вложить свои деньги под более высокий процент.

Причём, опять же, наиболее вырастут в цене именно облигации с большим значением дюрации (со сроком погашения через 10 лет).

Дюрация облигации: расчет, формула

Величина дюрации может быть использована для характеристики многих инвестиционных инструментов, но чаще всего ее применяют для учета рисков при использовании ценных бумаг с установленным сроком обращения.

Наиболее распространенным использованием показателя дюрации является расчет дюрации облигации. Как уже было приведено выше, дюрация облигации идентична общему понятию дюрации, что представляет собой определенное количество лет, необходимое на погашение полной стоимости облигации.

Облигация является эмиссионной долговой ценной бумагой и ее рыночная стоимость может меняться в течение периода ее полного погашения.

Дюрация позволяет инвестору в полной мере оценить финансовую привлекательность облигаций на рынке ценных бумаг, учитывая сразу несколько важных показателей — срок, на который выдана облигация, ставку процента (купон), номинальную стоимость ценной бумаги. Вычисленный показатель дюрации облигации поможет инвесторам принять решение о размещении портфеля ценных бумаг с наибольшей прибылью.

Расчет дюрации ценной бумаги может быть произведен несколькими способами:

Формула дюрации — как подсчитать значение

Дюрация зависит от трех составляющих: цена, процентная ставка и срока до погашения

De = /

Где:

• De – значение эффективной дюрации облигации
• Pi- – рыночная цена при понижении ставки
• Pi+ – рыночная цена при возрастании ставки
• Pr – номинальная цена ценной бумаги
• i+ – повышенная стартовая ставка
• i— – сниженная стартовая ставка

Считать самостоятельно дюрацию облигации по формуле не нужно. Она уже подсчитана автоматически. Данные можно посмотреть в торговом терминале QUIK или в открытых источниках по облигациям: https://www.rusbonds.ru (например).

Сложность формулы заключается в том, что текущие деньги не равны завтрашним деньгам. Поэтому для точности расчётов их следует дисконтировать.

Есть также другая формула дюрации, которая учитывает еще и ставку дисконтирования:

D = / (1+i)t) + ( / (1+i)n)] / p

Где:

• n – число платежей
• t – период, требуемый для полного погашения
• M – погашение номинальной цены облигации
• C – денежные поступления процентной прибыли
• i – ставка дисконтирования
• p – рыночная цена облигации

Дюрация Маколея

Фредерик Маколей вывел формулу вычисления дюрации еще в 30-х годах прошлого столетия, однако практическое использование в России ее началось только с 1993 г.

Формула выглядит следующим образом:

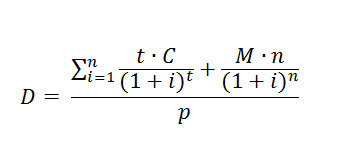
• где D – дюрация,
• n – количество платежей,
• t – время, необходимое для полного погашения,
• M – погашение номинальной стоимости ценной бумаги,
• С – денежный поток процентных доходов,
• i – ставка дисконтирования,
• p – рыночная стоимость ценной бумаги

К примеру, инвестор имеет две облигации номинальной стоимостью 5000 рублей каждая, при этом одна из них с нулевым купоном (бескупонная) и сроком погашения 3 года, другая с купоном, равным 5 %, который выплачивается ежегодно, сроком погашения также 3 года.

В первом случае дюрация будет равна сроку погашения облигации, а именно 3 года, так как денежный поток процентных доходов равен 0.

Во втором случае расчет можно произвести следующим образом:

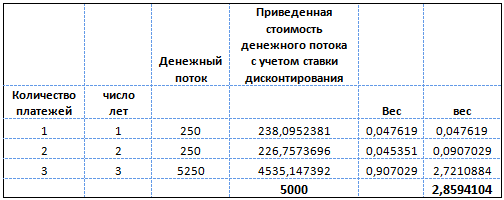
Дюрация облигации с 5 % купоном составит 2,86 года.

Модифицированная дюрация

В случае если процентная ставка доходности меняется в каком-либо временном промежутке до момента полного погашения номинальной стоимости, то необходимо использовать для расчета формулу модифицированной дюрации:

Dm= D/(1+ Cm/n)

• где Dm – модифицированная дюрация,
• Cm – доходность до погашения,
• n – количество выплат по купонам в год

Применяя предыдущий расчет, вычислим Dm= 2.86/((1+0.05/1))=2.86/1.05=2.72

Таким образом, при увеличении дохода по купону, дюрация снижается.

Однако, модифицированная дюрация применима лишь в том случае, если доходные денежные потоки с изменением процентной ставки не меняются, что в практическом применении чаще всего невозможно. Для расчета необходим более чувствительный инструмент к колебаниям ставки процента и, соответственно, доходности, каким и является эффективная дюрация.

Эффективная дюрация

При расчете эффективной дюрации облигации учитываются колебания процентных ставок как в сторону уменьшения, так и в сторону увеличения. Формула для расчета выглядит следующим образом:

• Где De – эффективная дюрация,
• Pi- — стоимость облигации при уменьшении процентной ставки,
• Pi+ — стоимость облигации при увеличении процентной ставки,
• Ро – начальная стоимость облигации,
• i+ — увеличенная начальная процентная ставка,
• i- — уменьшенная начальная процентная ставка.

Расчет эффективной дюрации применим с использование биноминального процентного дерева для исчисления стоимости облигации с учетом колебаний процентных ставок.

Понятие и значение для выбора облигаций

Полная информация об актуальных стратегиях, которые уже принесли миллионы пассивного дохода инвесторам

Скачать книгу

В описании облигации отдельно есть параметр “срок до погашения” и отдельно “дюрация”. Вроде бы и первый, и второй показывает, сколько осталось времени до возврата денег. Но цифры не всегда совпадают. Если в первом случае это простой срок до погашения, то во втором – с учетом купонов, амортизации, оферты.

В банковской терминологии есть термин “эффективная процентная ставка”, т. е. ставка с учетом капитализации процентов. Слово “эффективный” можно применить и к сроку возврата денег по облигации, т. к. он тоже учитывает разные характеристики ценной бумаги.

Формулу расчета в буквенном изображении я не буду приводить, чтобы не спугнуть начинающих инвесторов и не отбить у них желания покупать долговые ценные бумаги. Вам не придется по ней считать эффективный срок. Есть специальные ресурсы, где все уже подсчитано. О них поговорим отдельно в статье.

Но для понимания показателя предложу вам упрощенный вариант формулы в текстовом виде:

Дюрация (Д) = Сумма выплат (купоны или погашение номинала) * Время выплаты / Сумму выплат

Пример. Есть две облигации А и Б с одинаковой доходностью 5 % годовых. Номинал у обеих – 1 000 ₽. Срок до погашения – 3 года. У бумаги А купоны выплачиваются 1 раз в год. У бумаги Б – в конце срока вместе с погашением номинала. Денежные потоки по годам приведены в таблице.

Срок	Погашение номинала	Выплата купона
А
1		50
2		50
3	1 000	50
Итого	1 000	150
Б
1
2
3	1 000	150
Итого	1 000	150

Д (А) = (50 * 1 + 50 * 2 + 1050 * 3) / 1 150 = 2,87 года

Д (Б) = 1 150 * 3 / 1 150 = 3 года

Дюрация в первом случае меньше за счет более частых выплат купонов. Следовательно, меньше и риск. Инвестор быстрее получает возврат средств. Деньги можно опять пустить в инвестиции и заработать. А дюрация бескупонной облигации равна сроку погашения.

При прочих равных условиях лучше выбирать бумаги с меньшей дюрацией, т. к. меньше риск потери капитала. Кроме того, дюрация показывает не только средний срок возврата денег, но и зависимость цены облигации от изменения ключевой ставки Центробанка. Об этом мы тоже еще поговорим.

Можно проследить определенные свойства дюрации. Она применяется для сравнения долговых бумаг между собой и учитывает 4 основных фактора:

1. Срок до погашения. Чем больше срок до погашения, тем выше дюрация.
2. Амортизация. У долгового инструмента с амортизацией при прочих равных условиях дюрация ниже.
3. Размер и периодичность выплаты купонов. Чем больше размер купона и чаще выплаты, тем ниже дюрация.
4. Влияние изменения ключевой ставки Центробанка на цену облигации тем ниже, чем меньше срок до погашения и ниже дюрация.

Эффективный срок возврата рассчитывают только для бумаг с постоянным купоном, когда известно, в какие сроки и в каком размере будут выплаты.

Можно провести аналогию с банками. Погашение по кредиту они требуют с заемщиков проводить ежемесячно, тем самым снижают эффективный срок возврата долга за счет более частых платежей и, соответственно, уменьшают свои риски.

Примеры применения на практике

Теперь пришло время поговорить о том, для чего же всё-таки нужно знать такой параметр как ДО, и как его можно применять на практике.

Снижение риска инвестиций

Во-первых, как уже упоминалось выше, дюрация может служить мерой рискованности ваших инвестиций. Чем меньше величина дюрации (читай – срок окупаемости), тем меньше и риск потерять вложенные средства (или часть из них).

Для иллюстрации этого момента давайте рассмотрим простой пример. Представьте себе, что к вам пришли два человека, каждый с просьбой одолжить ему сумму в 1000000 рублей на срок в один год. Каждый из них готов уплачивать проценты в размере 15% годовых, но первый заёмщик готов платить проценты ежемесячно (а размере 15%/12 месяцев = 1,25%), а второй только по истечении года. Кому из них, при прочих равных условиях, вы предпочтёте одолжить деньги?

Ответ очевиден, наиболее выгодным для вас вариантом является одолжить деньги первому заёмщику, который согласен платить проценты ежемесячно. Этот вариант обладает тем неоспоримым преимуществом, что вы начинаете получать возврат инвестированных средств с первого же месяца. А это в свою очередь снижает риск инвестиций (ведь при одинаково неблагоприятном стечении обстоятельств, с первого заёмщика вы получите хоть что-то, в то время как со второго рискуете не получить вообще ничего).

Теперь перейдём к облигациям. Предположим, вы выбираете между двумя облигациями с одинаковыми сроками погашения и стоимостью. Но первая из этих облигаций предполагает выплату купонного дохода раз в месяц, а вторая только раз в год. Соответственно, ДО для первой облигации будет меньше, чем для второй (мы ведь помним, что ДО тем меньше, чем чаще выплачивается купонный доход по ней). И, следовательно, риск инвестиций в первые облигации будет меньшим, чем риск инвестиций во вторые облигации.

Зависимость ДО от процентной ставки

Облигации в целом являются довольно консервативным финансовым инструментом, то есть риск по ним и так минимален (он практически сопоставим с рисками по банковским депозитам). Поэтому дюрацию облигаций чаще рассматривают не в контексте снижения риска, а в контексте зависимости от процентных ставок.

Чтобы проиллюстрировать эту зависимость, давайте рассмотрим простой пример. Предположим, что вы приобрели, на одинаковые суммы денег, два вида облигаций одного и того же эмитента, но с разными сроками погашения. У первых срок погашения через год (ДО меньше), у вторых срок погашения через 10 лет (следовательно, ДО гораздо больше). Купонный доход по обоим видам облигаций составляет 10% годовых.

Теперь предположим, что процентные ставки в стране начали сильно расти и если сегодня выпускали облигации доходностью в 10%, то через некоторое время появляются новые облигации дающие доходность в 12%, а затем и в 15% и в 20%. Как вы думаете, при этом изменится стоимость ваших облигаций дающих 10% годового дохода? Правильно, их стоимость упадет, поскольку спрос на них значительно снизится (зачем людям покупать ваши «десятипроцентные» облигации по прежней цене, если они могут вложить деньги в более доходные бумаги).

Причём стоимость облигаций с большим значением ДО (у которых срок погашения через 10 лет) снизится гораздо больше, чем стоимость облигаций с меньшим значением дюрации (у которых срок погашения через год).

Представим теперь, что события стали развиваться диаметрально противоположным образом и процентные ставки в стране начали падать. То есть если сегодня вложить деньги под 10% годовых можно было относительно легко, то через некоторое время процентная ставка снизится до 5% и вложить деньги под те же 10% (с сохранением того же уровня риска) уже будет попросту невозможно. Очевидно, что при этом варианте развития событий, ваши облигации значительно вырастут в цене, ведь каждый предпочтёт вложить свои деньги под более высокий процент.

Причём, опять же, наиболее вырастут в цене именно облигации с большим значением дюрации (со сроком погашения через 10 лет).

Примеры дюрации

1. Возьмем две облигации: дисконтную и обычную купонную. Первая покупается с дисконтом (например, за 700 рублей), а в конце срока действия облигации возвращается номинал (1000 рублей). До конца срока действия дисконтной бумаги инвестор ничего не получает — поэтому дюрация в этом случае равна сроку, через который будет погашен выпуск.

Обычная же облигация платит купоны, т.е. возвращает инвестору часть вложенной суммы до своего погашения. Если представить, то обе облигации выпущены сроком на 10 лет и через 5 объявляют дефолт, то в случае выпуска с дисконтом инвестор не получит ничего, а во втором случае компенсирует часть вложенных средств купонами. Например, при купоне 10% годовых через 5 лет инвестор вернет половину инвестиций. Другими словами: в случае купонной облигации дюрация всегда меньше срока ее обращения.

2. Другая ситуация: две купонные облигации с одинаковым купоном, но разным сроком обращения: 3 года и 10 лет. Понятно, что в первом случае инвестор быстрее получит тело депозита назад — так что дюрация в первом случае ниже.

3. Еще один случай: срок действия и доходность к погашению облигаций одинакова, но ставка купонов по ним разная: например 3 и 6%. В этом случае можно ожидать более низкой дюрации от бумаги с более высоким купоном, так как он ускоряет окупаемость.

4. Кроме того, можно рассмотреть случай бессрочной облигации, которая может никогда не вернуть тело депозита, но обещает исправно выплачивать купон. Тут показатель можно вычислить только из купонов — например, при ставке 10% годовых инвестору потребуется 10 лет (3650 дней), чтобы окупить свои инвестиции.

ГКО – первые дисконтные облигации в России

В 1993 году Россия выпустила первые дисконтные облигации, которые получили наименование «государственные краткосрочные облигации» (ГКО). Их номинал начинался от 10 рублей, эмитентом выступал Минфин, а размещением выпусков на ММВБ занимался Центробанк. Срок обращения ГКО был фиксированный: 3, 6 или 12 месяцев.

Поначалу продажи шли со скрипом, но постепенно с ростом инфляции Минфин начал повышать их доходность, и уже скоро по ГКО можно было получать 100-250% годовых! Естественно, на них начался бешеный спрос, подстегиваемый галопирующей инфляцией.

Вскоре наши бравые экономисты превратили выпуск ГКО фактически в финансовую пирамиду: выплаты прежним покупателям обеспечивались за счет притока новых покупателей, процент рос и рос… В 1997 году на рынок ГКО был открыт доступ иностранным инвесторам, и захлебнувшаяся было пирамида вновь задышала: иностранцы уже давно облизывались на наши бескупонные облигации. Но приток новых инвесторов помог лишь на короткий срок.

В августе 1998 году государство объявило технический дефолт по ГКО, а затем и фактический по всем своим обязательствам. Пузырь лопнул. Что было потом – знаете сами (если не знаете – почитайте учебники истории).

В чем был неуспех ГКО:

• огромные проценты – государство просто не могло обеспечить такую доходность, и ему пришлось спешно печатать деньги, разгоняя инфляцию, и одновременно привлекать новых вкладчиков;
• ГКО были краткосрочные – привлеченные деньги просто не успевали влиться в экономику, они тут же тратились на выплаты по прежним облигациям;
• нулевыми облигациями активно торговали спекулянты, и спрос / предложение определялись не объективными экономическими причинами, а желанием отдельных личностей заработать побольше денег.

В результате имеем, что имеем.

В 1998 году Центробанк попытался воскресить дисконтные облигации в России, выпустив так называемые БОБР (бескупонные облигации Банка России). Они распространялись только среди других кредитно-финансовых учреждений и были недоступны простым смертным (т.е. физлицам). Но инициатива не получила поддержки. Сейчас БОБРы не выпускаются, на смену им пришли КОБРы.

Зависимость дюрации от процентной ставки

Облигация — рыночный инструмент. Ее котировки меняются, и в том числе зависят от уровня процентной ставки. Зависимость обратно пропорциональная: в случае роста процентной ставки котировки облигаций падают, а в случае падения ставки растут. Почему так происходит, я подробно объяснял здесь. Что это значит для дюрации?

Допустим, процентная ставка сейчас высока и вы ожидаете ее снижения. Как поступить в этом случае? Здесь оказывается выгодна бумага с более высокой дюрацией (т.е. большим сроком обращения). Почему? Падение ставки повысит цену облигации. Если предположить, что до снижения ставки она торговалась по номиналу, то теперь станет торговаться с премией. Например, в 105% от номинала. И чем выше будет дюрация, тем больше может быть рост.

Соответственно, в обратной ситуации ожидании роста ставки будет выгодна облигация с меньшей дюрацией (которая вообще несет меньше риска). Если ставка растет, то цена облигации падает. Но бумага с небольшой дюрацией быстрее вернется к номиналу, поскольку будет погашена, и скомпенсирует падение.

Модифицированная дюрация

Модифицированная дюрация связана с предыдущим пунктом и показывает «чувствительность» облигации к изменению ключевой ставки на 1 процент. Выше приведен скрин выпуска ОФЗ-26209 с дюрацией в 984 дня, т.е. 2.7 года. И прямо под ней рассчитан показатель модифицированной дюрации в 2.51%.

Итоги

Дюрация облигации – это то количество лет, спустя которое финансовый вкладчик сможет вернуть себе потраченные деньги, которые связаны с покупкой финансового инструмента назад.
Сроки погашения говорят нам, когда вы сможете получить свое денежное возмещение.
Дюрация способна наглядно продемонстрировать, когда вы сможете вернуть вложенные финансы.
Большая дюрация гласит о значительном риске, в отличие от небольшой дюрации ценной бумаги.
Важно учитывать то, что любая доходная облигация с достаточной дюрацией является более чувствительной к скачкам стоимости, что будет сильно зависеть от показателя процентной ставки.
Также стоит учитывать, что чем более значительная процентная ставка, тем более прибыльная будет ценная бумага. Кроме того, тем меньшим будет размер дальних выплат и слабее дюрация.
Дюрация облигации — это простыми словами временные сроки обращения ценной бумаги.
Понятие имеет два важнейших маркера для определения
Также сюда включается вероятность того, что поменяются процентные ставки на протяжении всего отрезка этого времени.
Общая суть дюрации заключается во временном периоде, спустя который хозяин выпущенной компанией облигации имеет возможность получить данную облигацию обратно в свои руки

Часто расчет проводится в годах, однако на отечественном рынке ценных бумаг такой расчет проводят в днях.
Дюрация облигации дает возможность увидеть временные сроки полного возвращения вложенных финансов в приобретение ценных бумаг.
При равнозначном уровнем дохода за одну ценную бумагу из двух, стоит выбирать облигацию с меньшей.
Чтобы приблизительно уравнять вероятности возврата денег по выданным клиентам кредитам, банки(и любые подобные учреждения) могут увеличивать процентные ставки.

Приведенная формула дюрации дает возможность грамотно оценить показатель рискованности своих вложений. Главная цель в работе любого вкладчика — сведение до наименьшего значения вероятности потерять свои средства. При этом ему необходимо оставить прежний уровень доходности или поднять его по возможности.